 |
A C. 1433. feladat (2017. szeptember) |
C. 1433. Egy csuklós szerkezet keresztmetszete négy darab \(\displaystyle r\) sugarú kör, és közöttük egy rombusz alakban kifeszülő négy, \(\displaystyle r\times6r\) oldalhosszúságú téglalap úgy, hogy a téglalapok \(\displaystyle r\) hosszú oldala érinti a kört. (Az érintési pont az oldal felezőpontjába esik.) A körök mozgatásával a rombusz szöge változhat, de a téglalapok nem lóghatnak egymásba. Mekkora a legkisebb és a legnagyobb lehetséges szög?
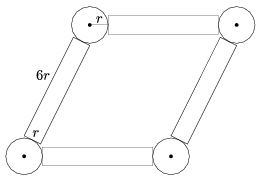
(5 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldás. A legkisebb szög akkor keletkezik, amikor a téglalapok csúcsa éppen összeér a \(\displaystyle C\) pontban.
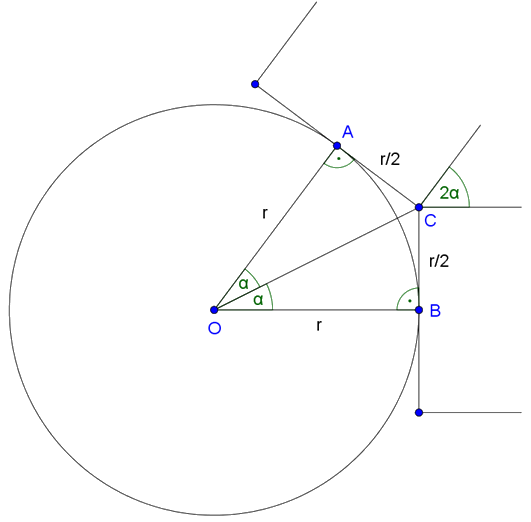
Mivel az érintők merőlegesek a sugárra és a téglalap szögei derékszögek, így a rombusz hegyesszöge megegyezik az \(\displaystyle AOB∡=2α\) szöggel (párhuzamos szárú hegyesszögek).
Az \(\displaystyle ACO\) és \(\displaystyle BCO\) egybevágó derékszögű háromszögekben a rövidebbik befogók: \(\displaystyle AC=BC=r/2\), a hosszabbik befogók: \(\displaystyle AO=BO=r\). Így \(\displaystyle tgα=1/2\), vagyis \(\displaystyle α≈26,565°\). Tehát a legkisebb szög \(\displaystyle 2α≈53,13°\). A legnagyobb szög is ekkor keletkezik, ugyanezen rombusz tompaszöge lesz az: \(\displaystyle 180°-2α=126,87°\).
Statisztika:
99 dolgozat érkezett. 5 pontot kapott: Agócs Katinka, Ajtai Boglárka, Almási Adél Csilla, Bukor Benedek, Csikós-Nagy Máté, Dékány Barnabás, Gálffy Veronika, Jankovits András, Kocsák Boglárka, Kozma Balázs, Kozma Bianka, Kulcsár Krisztina, Lajkó Áron, Magyar 257 Boglárka, Mészáros 916 Márton, Mészáros Melinda, Molnár 410 István, Molnár 921 Ádám, Mónos Péter, Németh Csilla Márta, Oláh Zsolt, Paksi Barnabás, Pap Ábel, Porkoláb Mercédesz, Remény Olivér, Rittgasszer Ákos, Ruszthi Csilla, Spányik Teodor, Surján Anett, Szalkai Tamás, Szécsi Adél Lilla, Szepessy Luca, Takács 666 Réka, Tirpák Péter, Török Boldizsár, Veress Luca. 4 pontot kapott: 35 versenyző. 3 pontot kapott: 16 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2017. szeptemberi matematika feladatai

