A C. 1435. feladat (2017. október)

C. 1435. Egy 2 egység oldalú négyzet két szomszédos oldala, mint átmérő fölé befelé félköröket rajzolunk. Határozzuk meg az egyik félkört és a négyzet oldalát belülről érintő, a másik félkört pedig kívülről érintő kör sugarát.

Javasolta: Fülöp Dóra (Pécs)

(5 pont)

A beküldési határidő 2017. november 10-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit. A félkörök sugarai \(\displaystyle R=\frac a2=1\) hosszúak. A kis érintő kör sugara legyen \(\displaystyle r\), a \(\displaystyle HE\) szakasz hossza pedig \(\displaystyle x\). Az érintésekből következik, hogy \(\displaystyle GE=R-r=1-r\), \(\displaystyle GF=R+r=1+r\).

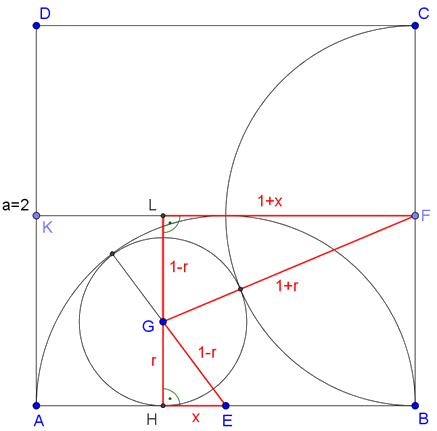
Mivel \(\displaystyle E\), \(\displaystyle F\) és \(\displaystyle K\) a négyzet egy-egy oldalának felezőpontja, és \(\displaystyle HL||BF\), valamint \(\displaystyle KF||AB\), ezért \(\displaystyle GL=R-r=1-r\) és \(\displaystyle FL=R+x=1+x\).

Írjuk fel a Pitagorasz-tételt az \(\displaystyle EGH\) és \(\displaystyle FGL\) derékszögű háromszögekben:

\(\displaystyle (1-r)^2=x^2+r^2,\)

\(\displaystyle (1+r)^2=(1-r)^2+(1+x)^2.\)

Elvégezve a műveleteket és rendezve:

\(\displaystyle 1-x^2=2r,\)

\(\displaystyle 4r=x^2+2x+1.\)

\(\displaystyle 2r\) értékét az első egyenletből a másodikba beírva és rendezve:

\(\displaystyle 2-2x^2=x^2+2x+1,\)

\(\displaystyle 0=3x^2+2x-1.\)

A másodfokú egyenlet pozitív megoldása: \(\displaystyle x=\frac 13\), amiből \(\displaystyle r=\frac{1-x^2}{2}=\frac{1-\frac19}{2}=\frac49\).

A kapott megoldások kielégítik a fenti egyenletrendszert.

Tehát a keresett kör sugara \(\displaystyle r=\frac49\).

Statisztika:

101 dolgozat érkezett.
5 pontot kapott:	69 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	4 versenyző.
0 pontot kapott:	17 versenyző.

A KöMaL 2017. októberi matematika feladatai