 |
A C. 1440. feladat (2017. október) |
C. 1440. Az \(\displaystyle ABCDA'B'C'D'\) egységkockában legyenek \(\displaystyle M\) és \(\displaystyle N\) a \(\displaystyle D'\) és \(\displaystyle B\) pontok merőleges vetületei a \(\displaystyle B'D\) testátlóra. Határozzuk meg a \(\displaystyle BND'M\) négyszög területét.
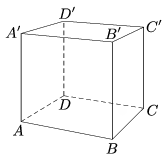
Matlap (Kolozsvár)
(5 pont)
A beküldési határidő 2017. november 10-én LEJÁRT.
Megoldás. \(\displaystyle DD’=BB’=1\) és \(\displaystyle DB=D’B’=\sqrt2\). Ebből \(\displaystyle DB’=\sqrt{1^2+(\sqrt2)^2}=\sqrt 3\).
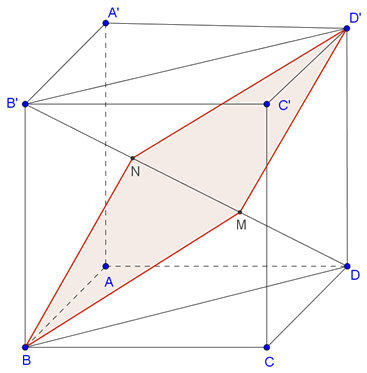
A derékszögű \(\displaystyle DB’D’\) háromszögben használjuk a befogó tételt: \(\displaystyle DD’^2=DM\cdot DB'\), amiből \(\displaystyle DM=\frac{DD’^2}{DB'}=\frac{1}{\sqrt3}= \frac{\sqrt3}{3}\). A szimmetria miatt \(\displaystyle B’N=\frac{\sqrt3}{3}\).
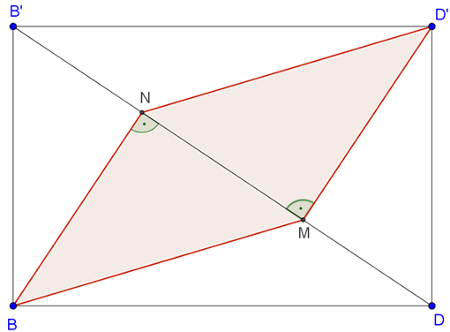
\(\displaystyle MN=DB’-DM-B’N=\sqrt3-\frac{\sqrt3}{3}-\frac{\sqrt3}{3}=\frac{\sqrt3}{3}=\frac{B'D}{3}.\)
\(\displaystyle T_{BND'M}=2\cdot T_{ND'M}= 2\cdot\frac13 T_{B'D'D}= \frac23\cdot\frac{1\cdot\sqrt2}{2}=\frac{\sqrt2}{3}.\)
Statisztika:
100 dolgozat érkezett. 5 pontot kapott: Agócs Katinka, Ajtai Boglárka, Almási Adél Csilla, Balog 518 Lóránd, Baráth Bettina, Bíró Dániel, Börcsök Barnabás, Bukor Benedek, Bulyáki Soma, Csilling Eszter, Deák Péter, Debreczeni Tibor, Dézsi Viktória, Dócs Bernadett, Gálffy Veronika, Gárdonyi Csilla Dóra, Görcs András, Gréczi Gergely Ádám, Gulyás Bálint, Háder Márk István, Halász Mihály, Hegedűs András, Jávorka Marcell, Kaposi Benedek, Kovács 111 Bence, Kovács 161 Márton Soma, Kulcsár Krisztina, Kún Hanga, Magyar 257 Boglárka, Mester Gyöngyvér, Mészáros 916 Márton, Mészáros Melinda, Misik Márton, Molnár 410 István, Molnár 921 Ádám, Németh Csilla Márta, Pszota Máté, Rittgasszer Ákos, Spányik Teodor, Surján Anett, Szántó Dániel, Szécsi Adél Lilla, Szepessy Luca, Tóth 411 Zoltán, Varga 269 Viktor, Varga Dániel Jonatán. 4 pontot kapott: 22 versenyző. 3 pontot kapott: 17 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. októberi matematika feladatai

