 |
A C. 1441. feladat (2017. november) |
C. 1441. Egy kávézóban különböző alapanyagokból különböző kávékülönlegességeket készítenek. Tudjuk, hogy az itallapon szereplő bármely kávét kiválasztva pontosan három olyan másik kávét találhatunk, amelynek a kiválasztottal van közös alapanyaga. Azt is tudjuk, hogy ha két kávénak nincs, akkor található hozzájuk egy harmadik, amellyel mindkettőnek van közös alapanyaga. Legfeljebb hány különböző kávékülönlegesség lehet az itallapon?
(5 pont)
A beküldési határidő 2017. december 11-én LEJÁRT.
Megoldás. Legyenek az itallapon szereplő kávék egy egyszerű gráf csúcspontjai. Ha két kávénak van közös alapanyaga, akkor az ezeknek megfelelő csúcsokat kössük össze egy éllel. Az első feltétel pontosan azt jelenti, hogy a gráf minden csúcsának 3 a fokszáma, tehát minden csúcsból 3 él indul.
A második feltétel azt mondja ki, hogy ha két csúcsot nem köt össze él, akkor van olyan csúcs, amivel mindkettő össze van kötve. Ez pontosan azt jelenti, hogy bármely csúcsból bármely másik csúcsba legfeljebb két élen keresztül eljuthatunk.
Legyen a gráf egyik csúcsa \(\displaystyle A\), melyből egy-egy él vezet a \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) csúcsokba. Minden további \(\displaystyle X\) csúcsból kell vezetnie élnek a \(\displaystyle B\), \(\displaystyle C\) vagy \(\displaystyle D\) pontok valamelyikébe, különben az \(\displaystyle A\) és \(\displaystyle X\) csúcsokra nem teljesül a második feltétel.
A \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) csúcsokból \(\displaystyle A\)-n kívül még 2-2 csúcsba vezethet él, tehát az eddigi 4 csúcson kívül még legfeljebb \(\displaystyle 3\cdot2=6\) csúcsa lehet a gráfnak.
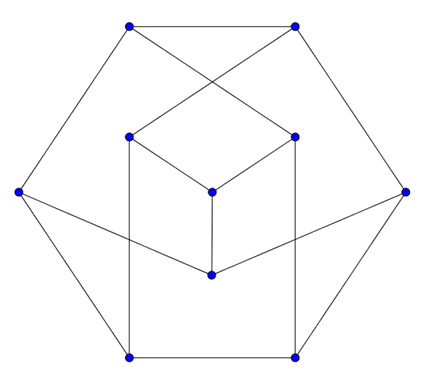
Ilyen 10 csúcsú gráf létezik (lásd az ábrát). Így legfeljebb 10 kávékülönlegesség lehet az itallapon.
Statisztika:
89 dolgozat érkezett. 5 pontot kapott: Ács Imre, Biró 424 Ádám, Czett Mátyás, Hámori Janka, Jánosdeák Márk, Kerekes Boldizsár, Koleszár Domonkos, Kovács 124 Kinga, Markó Gábor, Pinke Andrea, Shuborno Das, Sike 912 András, Szalontai Kinga Sára, Werner András, Williams Hajna. 4 pontot kapott: Bottlik Domonkos, Fonyi Máté Sándor, Forczek Bianka, Forgács Kata, Szente Péter. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 19 versenyző. 1 pontot kapott: 22 versenyző. 0 pontot kapott: 19 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2017. novemberi matematika feladatai
