 |
A C. 1445. feladat (2017. november) |
C. 1445. Az ,,Egy angol, aki dombra ment fel, de hegyről jött le'' című filmben egy walesi falu mellett lévő hegyet, miután lemérték a magasságát, a földmérők dombnak minősítettek. A falusiak büszkék voltak a hegyükre, és ebbe nem nyugodtak bele. Elhatározták, hogy 984 lábról 1004 lábra emelik a magasságát. Földet hordanak fel a 82 láb sugarú félgömbnek tekinthető dombtetőre olyan csonkakúp alakban, amelynek alkotója a félgömb érintője, és \(\displaystyle 45^\circ\)-os szöget zár be a vízszintessel. Így a magasság meghaladja majd az 1000 lábat, és a dombot újra hegynek lehet nevezni. Hány köbláb földet kellett felhordaniuk a dombra?
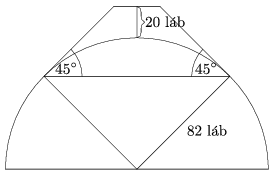
(5 pont)
A beküldési határidő 2017. december 11-én LEJÁRT.
Megoldás. Használjuk az ábra jelöléseit.
A hiányzó föld térfogata egy csonkakúp és egy gömbszelet térfogatának különbsége.
A csonkakúp síkmetszete az ábrán az \(\displaystyle ABCD\) trapéz, a gömbszeleté pedig az \(\displaystyle ABG\) körszelet. A mértékegység a hosszúságoknál mindenütt láb.
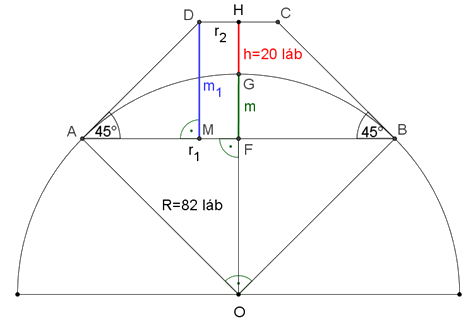
Mivel \(\displaystyle AD\) érintő, ezért \(\displaystyle DAO\angle=90^{\circ}\) és így \(\displaystyle FAO\angle=45^{\circ}\). Tehát az \(\displaystyle AFO\) egyenlő szárú derékszögű háromszög, ezért \(\displaystyle FO=FA=\frac{R}{\sqrt2}=\frac{82}{\sqrt2}=41\sqrt2\).
A gömbszelet magassága \(\displaystyle m=R-FO=82-41\sqrt2≈24,017\), sugara \(\displaystyle r_1=FA=41\sqrt2≈57,983\).
A gömbszelet térfogata: \(\displaystyle V_{gsz}=\frac{πm(3r_1^2+m^2)}{6}≈134088,9\).
A csonkakúp alapkörének sugara szintén \(\displaystyle r_1≈57,983\), magassága \(\displaystyle m_1=m+h=82-41\sqrt2+20=102-41\sqrt2≈44,017\).
Az \(\displaystyle ADM\) egyenlő szárú derékszögű háromszög, ezért \(\displaystyle AM=DM= m_1\).
A csonkakúp fedőkörének sugara \(\displaystyle r_2=DH=MF=AF-AM=r_1-m_1≈13,966\).
A csonkakúp térfogata: \(\displaystyle V_{cs}=\frac{πm_1(r_1^2+r_1 r_2+r_2^2)}{3}≈201288,6\).
A szükséges föld térfogata: \(\displaystyle V_F=V_{cs}-V_{gsz}≈67200\) köbláb.
Statisztika:
166 dolgozat érkezett. 5 pontot kapott: 65 versenyző. 4 pontot kapott: 42 versenyző. 3 pontot kapott: 24 versenyző. 2 pontot kapott: 18 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 9 dolgozat.
A KöMaL 2017. novemberi matematika feladatai
