 |
A C. 1459. feladat (2018. január) |
C. 1459. Tükrözzük az \(\displaystyle y=x^2\) egyenletű normál parabolát az \(\displaystyle F\left(0;\frac 14\right)\) pontra. Mekkora szögben metszi egymást a két parabola?
(5 pont)
A beküldési határidő 2018. február 12-én LEJÁRT.
Megoldás. Az \(\displaystyle y=x^2\) parabolát a \(\displaystyle \left(0;\frac14\right)\) pontra tükrözve az \(\displaystyle y=-x^2+\frac12\) parabolát kapjuk.
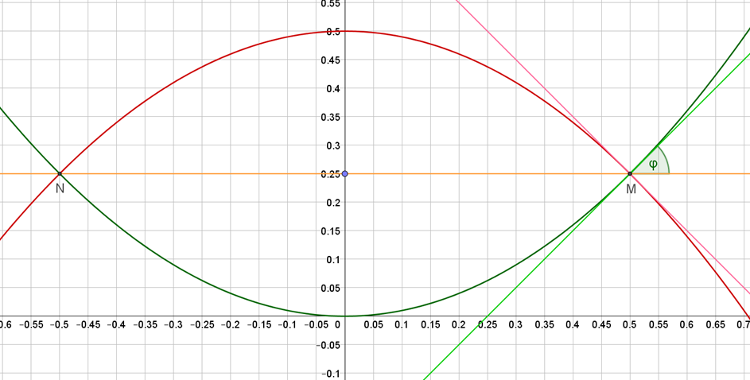
A metszéspontok \(\displaystyle x\) koordinátáit az \(\displaystyle x^2=-x^2+\frac12\) egyenletből kapjuk. Rendezve: \(\displaystyle x^2=\frac14\), amiből \(\displaystyle x_1=\frac12\), \(\displaystyle x_2=-\frac12\). Így a metszéspontok koordinátái: \(\displaystyle M\left(\frac12;\frac14\right)\) és \(\displaystyle N\left(-\frac12;\frac14\right)\).
Ha meghatározzuk az \(\displaystyle M\) pontban az \(\displaystyle y=x^2\) parabola érintőjének \(\displaystyle φ\) irányszögét, akkor a szimmetria miatt az érintők által bezárt szög az \(\displaystyle M\) és \(\displaystyle N\) pontban is \(\displaystyle 2φ\) lesz.
Legyen a keresett érintő egyenlete: \(\displaystyle y=mx+b\). Mivel átmegy az \(\displaystyle M\left(\frac12;\frac14\right)\) ponton, ezért egyenlete \(\displaystyle \frac14=\frac12 m+b\), amiből \(\displaystyle b=-\frac12 m+\frac14\). Ezt visszahelyettesítve:
\(\displaystyle y=mx-\frac12 m+\frac14.\)
Ha ez érintője az \(\displaystyle y=x^2\) parabolának, akkor az \(\displaystyle x^2=mx-\frac12 m+\frac14\) másodfokú egyenletnek csak egy megoldása van. Rendezve: \(\displaystyle x^2- mx+\frac12 m-\frac14=0\). Pontosan akkor van egy megoldása, ha a diszkrimináns értéke nulla: \(\displaystyle D=m^2-2m+1=0\), vagyis \(\displaystyle (m-1)^2=0\). Tehát az érintő meredeksége \(\displaystyle m=1\).
\(\displaystyle \tgφ=1\), vagyis az irányszög \(\displaystyle φ=45°\). Az érintők által, vagyis a két parabola által bezárt szög \(\displaystyle 2φ=90°\).
Statisztika:
126 dolgozat érkezett. 5 pontot kapott: 62 versenyző. 4 pontot kapott: 11 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 32 versenyző.
A KöMaL 2018. januári matematika feladatai

