 |
A C. 1460. feladat (2018. január) |
C. 1460. Egy speciális, forgásszimmetrikus hópehely képződése a következőképpen zajlik: minden másodpercben a hópehely végződéseinek felezőpontjából indulva két, egyenként harmadakkora új végződés keletkezik. (A hópehely kiinduló állapota és a képződés első két lépése az ábrán látható.) Hány darab 10 mikrométer hosszúságú végződése lesz a hópehelynek 6 másodperc elteltével, ha a hópehely átmérője 4,32 mm?
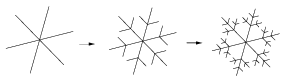
(5 pont)
A beküldési határidő 2018. február 12-én LEJÁRT.
Megoldás. A hat ág közül elég egyet vizsgálni. Nézzük meg, mi történik egy másodpercben ezen az egy ágon.
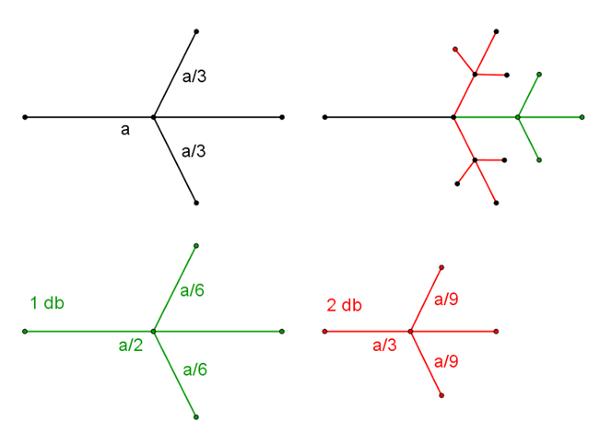
Minden, az előző másodperc végén létező ágból létrejön egy feleakkora és két harmad akkora ág. Tehát, amikor a végződések hossza feleződik, akkor egy ág keletkezik, amikor harmadolódik, akkor pedig kettő.
Kezdetben egy ág hossza az átmérő fele: \(\displaystyle 2,16~\mathrm{mm}=2160~\mathrm{μm}\). A \(\displaystyle 10\) μm hosszú végződések számát keressük.
\(\displaystyle \frac{10}{2160}=\frac{1}{216}=\left(\frac12\right)^3\cdot\left(\frac13\right)^3.\)
Ez azt jelenti, hogy a \(\displaystyle 10\) μm-es végződéshez \(\displaystyle 3\)-szor választjuk a felező lehetőséget, ahol egy ág keletkezik és \(\displaystyle 3\)-szor a harmadoló lehetőséget, ahol kettő.
A \(\displaystyle 6\) lehetőségből 6alatt a \(\displaystyle 3\)-féleképpen választhatjuk ki, hogy mikor legyen a harmadolás, ez \(\displaystyle 20\) lehetőség, viszont a harmadoló ágakból mindig kettő van, így ezt szoroznunk kell még \(\displaystyle 2^3\)-nal. Ezért egy ágon \(\displaystyle 160\) db \(\displaystyle 10\) μm-es végződés lesz \(\displaystyle 6\) sec elteltével.
Az egész hópelyhen ennek \(\displaystyle 6\)-szorosa, vagyis \(\displaystyle 960\) darab.
Statisztika:
52 dolgozat érkezett. 5 pontot kapott: Ajtai Boglárka, Almási Adél Csilla, Balog 518 Lóránd, Böcskei Bálint Attila, Bukor Benedek, Debreczeni Ákos, Debreczeni Tibor, Dékány Barnabás, Gárdonyi Csilla Dóra, Jankovits András, Kovács 161 Márton Soma, Lajkó Áron, Mészáros 916 Márton, Molnár 410 István, Németh Csilla Márta, Rittgasszer Ákos, Sal Dávid, Spányik Teodor, Surján Anett, Szajkó Szilvia, Szécsi Adél Lilla, Szűcs 865 Eszter, Vlaszov Artúr. 4 pontot kapott: Gálffy Veronika, Lénárd Kristóf, Tóth Imre, Wolff Vilmos. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 11 versenyző.
A KöMaL 2018. januári matematika feladatai

