Problem C. 1491. (September 2018)

C. 1491. The length of side \(\displaystyle AD\) of a rectangle \(\displaystyle ABCD\) is 1 cm. The angle bisector of \(\displaystyle \angle BAD\) and the perpendicular bisector of diagonal \(\displaystyle AC\) intersect on the side \(\displaystyle CD\). Find the exact length of side \(\displaystyle CD\).

(5 pont)

Deadline expired on October 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha \(\displaystyle AD=AB\), akkor a szögfelező egybeesik az \(\displaystyle AC\) átlóval, aminek a felező merőlegese a \(\displaystyle D\) pontban metszi a \(\displaystyle CD\) oldalt.

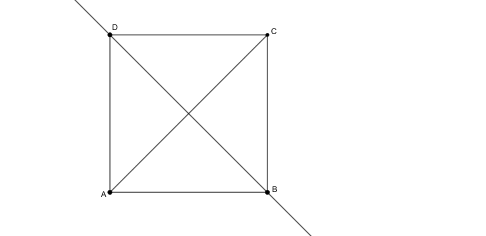
Ha \(\displaystyle AD>AB\), akkor az oldalfelező merőleges nem metszi a \(\displaystyle CD\) szakaszt.

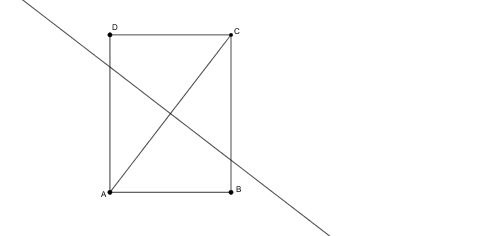
Legyen tehát \(\displaystyle AD<AB\) (ekkor a szögfelező az átló ,,felett" halad) és használjuk az ábra jelöléseit. Az \(\displaystyle AC\) átló felezőpontja legyen \(\displaystyle F\), a \(\displaystyle BAD∡\) szögfelezőjének és az \(\displaystyle AC\) átló felező merőlegesének metszéspontja pedig \(\displaystyle M\).

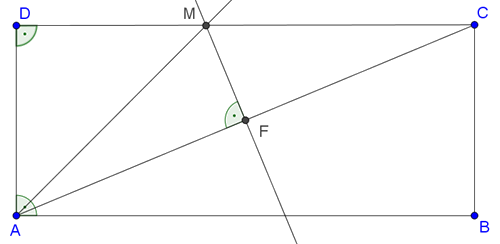
\(\displaystyle DAM∡=45°\), ezért \(\displaystyle ADM\) egyenlő szárú derékszögű háromszög: \(\displaystyle DM=AD=1\) cm. A háromszög átfogója pedig \(\displaystyle AM=\sqrt2\) cm.

Az \(\displaystyle AC\) átló \(\displaystyle FM\) felező merőlegese szimmetriatengely az \(\displaystyle AMC\) háromszögben, ezért \(\displaystyle MC=AM=\sqrt2\).

Mivel az \(\displaystyle M\) pont a \(\displaystyle DC\) oldalra esik, így \(\displaystyle DC=DM+MC=1+\sqrt2\).

Tehát a \(\displaystyle CD\) oldal pontos értéke: \(\displaystyle 1+\sqrt2\) cm.

Statistics:

268 students sent a solution.
5 points:	207 students.
4 points:	33 students.
3 points:	7 students.
2 points:	5 students.
1 point:	5 students.
0 point:	1 student.
Not shown because of missing birth date or parental permission:	10 solutions.

Problems in Mathematics of KöMaL, September 2018