 |
A C. 1492. feladat (2018. szeptember) |
C. 1492. Hányféleképpen juthatunk el az ábrán látható 15 egységkockából felépített test \(\displaystyle A\) csúcsából a \(\displaystyle B\) csúcsába rácsvonalak mentén, ha csak a három megjelölt irányba haladhatunk?
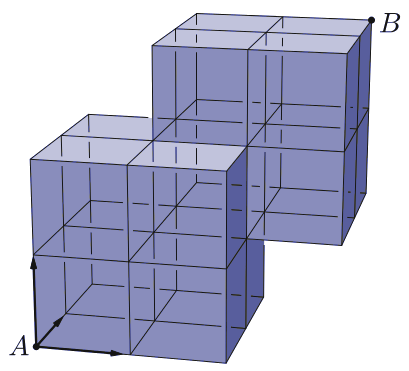
(5 pont)
A beküldési határidő 2018. október 10-én LEJÁRT.
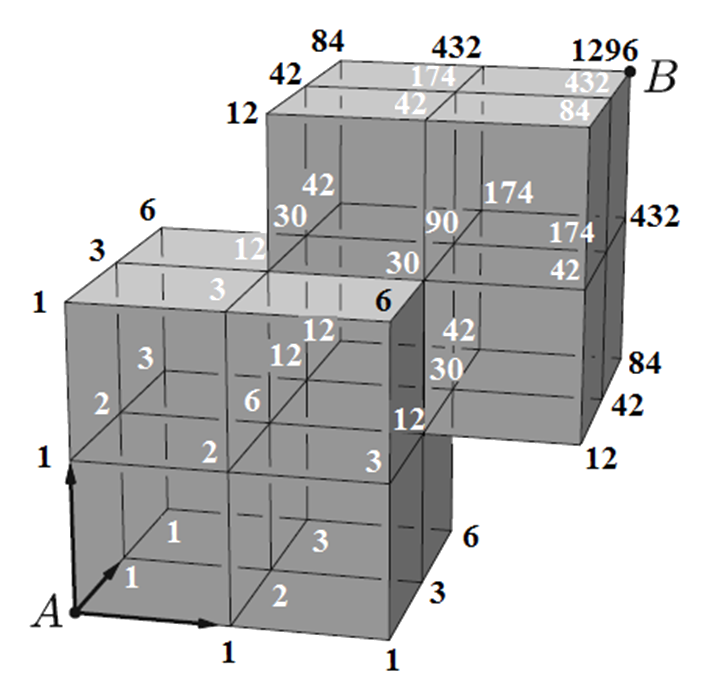
Megoldás. Írjuk oda minden csúcshoz, hogy hányféleképpen lehet oda eljutni: Az \(\displaystyle A\) csúcs szomszédjaiba 1-1-féleképpen; innentől kezdve minden csúcsban összeadjuk az oda vezető csúcsokra (melyből egy vagy kettő van) írt számokat.
Válasz: 1296.
Statisztika:
293 dolgozat érkezett. 5 pontot kapott: 166 versenyző. 4 pontot kapott: 9 versenyző. 3 pontot kapott: 21 versenyző. 2 pontot kapott: 18 versenyző. 1 pontot kapott: 11 versenyző. 0 pontot kapott: 60 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 8 dolgozat.
A KöMaL 2018. szeptemberi matematika feladatai

