A C. 1498. feladat (2018. október)

C. 1498. Milyen hosszú lehet legfeljebb egy 2 méter magas ember árnyéka a Földön? A Földet tekintsük egy 6370 km sugarú gömbnek, melyre a fénysugarak a Napból párhuzamosan érkeznek.

(5 pont)

A beküldési határidő 2018. november 12-én LEJÁRT.

Megoldás. Állítsuk a két méter magas embert a Föld felszínére. Ha a Nap nem pontosan az ember feje fölött delel, akkor van árnyék, amely az ember lábától indul. Ha a Föld sík volna, akkor az árnyék korlátlanul növekedne, ahogy a napsugarak egyre nagyobb szöget zárnak be a álló ember egyenesével, miközben a sík többi részét megvilágítják.

Ha a Földet gömbnek tekintjük, akkor az árnyék egy gömbfelületre vetül. Most is nő az árnyék hossza, ha a Nap az álló ember egyenesével egyre nagyobb szöget zár be. De nem nőhet korlátlanul, mivel egy bizonyos szög után az ember árnyékának csak egy része vetül a Földfelszínre, míg a Földgömb további részét maga a Föld árnyékolja. Az árnyék akkor a leghosszabb, ha a 2 méter magas ember feje fölött haladó fénysugár éppen érinti a Földet.

Használjuk az ábra jelöléseit. Az $\displaystyle AB$ szakasz árnyéka a Földön akkor a leghosszabb, ha a napsugár a $\displaystyle BE$ egyenes irányában érkezik. Ekkor az árnyék hossza az $\displaystyle AE$ ív hossza.

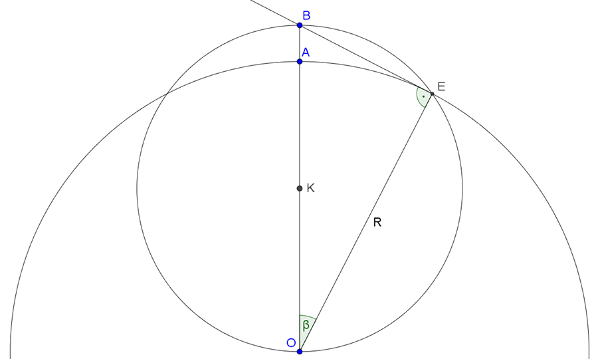
$\displaystyle OA=OE=R=6370000$ m, $\displaystyle AB=2$ m, és így $\displaystyle OB=6370002$ m.

Az $\displaystyle BEO$ derékszögű háromszögben legyen $\displaystyle BOE∡=β$. Ekkor $\displaystyle \cos β=\frac{OE}{OB}=\frac{6\,370\,000}{6\,370\,002}$, amiből $\displaystyle β≈0,000\,792\,43$ rad.

$\displaystyle \widehat{AE}=Rβ≈6\,370\,000~\textrm{m}\cdot0,000\,792\,43 ~\textrm{rad}≈5047,8~\textrm{m}.$

Megjegyzés. Ilyen kis szögeknél $\displaystyle β≈sinβ$, ezért $\displaystyle \widehat{AE}≈BE$. A $\displaystyle BE$ szakasz hosszát Pitagorasz-tétellel is számolhatjuk:

$\displaystyle BE=\sqrt{OB^2-OE^2}=\sqrt{6\,370\,002^2-6\,370\,000^2}≈5047,8~\textrm{m}.$

Statisztika:

178 dolgozat érkezett.
5 pontot kapott:	133 versenyző.
4 pontot kapott:	18 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	11 versenyző.
Nem versenyszerű:	4 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2018. októberi matematika feladatai