 |
A C. 1517. feladat (2018. december) |
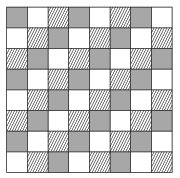
C. 1517. Egy sakktábla mezőit három színnel színeztük az ábrán látható módon. A táblán véletlenszerűen elhelyezünk egy huszárt, majd azzal véletlenszerűen (de szabályosan) egyet lépünk. Mekkora a valószínűsége annak, hogy a huszár a kiinduló mezővel azonos színű helyre érkezik?
(5 pont)
A beküldési határidő 2019. január 10-én LEJÁRT.
Megoldás. Az ábra szerint a három szín legyen fehér, szürke és csíkos. Először számoljuk meg, hogy melyik színű mezőből hány darab van:
Fehérből: \(\displaystyle 8+5+2+5+2=22\).
Szürkéből és csíkosból: \(\displaystyle 7+4+1+6+3=21\).
Most képzeljük el, hogy a huszár már a táblán van, és nézzük meg, hogy mekkora valószínűséggel lesz ugyanolyan színű mezőn 1 lépés után:
1. eset: A huszárt sarokmezőre tettük: innen 2 másik mezőre léphet, 2 aleset lehetséges:
a) fehér volt a sarokmező, ekkor mindegyik más színű, így 0 a vizsgált valószínűség.
b) nem fehér a sarokmező, ekkor mindegyik lépés azonos színű mezőre történik, azaz 1 a keresett valószínűség.
2. eset: A huszár szélső, sarokkal szomszédos mezőn van, ilyenkor 3 lehetséges lépése van:
a) ha ez a mező fehér, akkor 3 lépésből 2 azonos színűre történik, így \(\displaystyle \frac{2}{3}\),
b) ha ez a mező nem fehér, akkor 3 lehetséges lépésből 1 ,,jó'', azaz \(\displaystyle \frac{1}{3}\) a valószínűség.
3. eset: A huszár valamelyik egyéb szélső mezőn van: innen 4 lehetséges lépése van, amiből 2 a kiindulási mező színével megegyező mezőre történik, 2 pedig más színűre, azaz a keresett valószínűség \(\displaystyle \frac{1}{2}.\)
4. eset: A huszárt a 2./7. sorba/oszlopba tettük le, de nem szélső mezőre:
a) 2./7. sor 2./7. mezőjére tettük: 4 lehetséges lépése van, amiből 2 ,,jó'', azaz \(\displaystyle \frac{1}{2}\) itt is a valószínűség.
b) Többi esetben: 6 lehetséges lépése van, amiből 3 ,,jó'', azaz \(\displaystyle \frac{1}{2}\) itt is a valószínűség.
5. eset Egy belső mezőre tesszük a huszárt, olyanra, ami nem tartozik bele az 1-4. esetekbe: ilyenkor 8 lehetséges lépése van, amiből 4 jó, így itt is \(\displaystyle \frac{1}{2}\) a keresett valószínűség.
Ezután külön-külön végignézzük minden színre, hogy mennyi annak a valószínűsége, hogy az adott színű mezőre kerül a huszár, és hogy egyet lépve szintén az adott színű mezőn lesz:
I. eset: Annak a valószínűsége, hogy fehér mezőre helyezzük el a huszárt, és azonos (fehér) színűre lépett:
\(\displaystyle \frac{22}{64}\left(\frac{2}{22} \cdot 0+ \frac{4}{22} \cdot \frac{2}{3}+\frac{16}{22}\cdot \frac{1}{2}\right)=\frac{1}{6}.\)
II. eset: Szürke (vagy: III. eset: csíkos) mezőre kerül a huszár:
\(\displaystyle \frac{21}{64}\left(\frac{1}{21} \cdot 1+\frac{2}{21} \cdot \frac{1}{3}+\frac{18}{21} \cdot \frac{1}{2}\right)=\frac{1}{6}.\)
A keresett valószínűség ennek a 3 valószínűségnek az összege:
\(\displaystyle P=\frac{3}{6}=\frac{1}{2}.\)
Azaz \(\displaystyle \frac{1}{2}\) valószínűséggel lép ugyanolyan színű mezőre a huszár, mint amilyenre véletlenszerűen feltettük.
2. Megoldásvázlat. Tükrözzük az első sor felezőmerőlegesére a sakktáblát. Vegyük észre, hogy ekkor szabályos huszárlépés szabályos huszárlépésbe megy át, továbbá ,,jó'' lépés mindig ,,rossz'' lépésbe, ,,rossz'' lépés pedig mindig ,,jó'' lépésbe. Így tükrös pozícióban lévő mezőkre az azonos színű mezőre lépés valószínűségének összege mindig 1, vagyis a feladat kérdésére a válasz \(\displaystyle \frac{1}{2}\).
Megjegyzés. A leggyakoribb hiba annak feltételezése volt, hogy minden lépés azonos valószínűségű, és ennek megfelelően a keresett valószínűség a kedvező lépések és az összes lehetséges lépés számának hányadosa. Ez a feltételezés azonban nem teljesül. Mivel a kezdő mezők bármelyikének kiválasztása \(\displaystyle \frac{1}{64}\) valószínűségű, ezért azok a lépések valószínűbbek, melyek olyan mezőről indulnak ki, ahonnan kevesebb huszár lépés indul.
Statisztika:
63 dolgozat érkezett. 5 pontot kapott: Adravecz Balázs, Debreczeni Tibor, Demcsák Ágnes, Facskó Vince, Falvay Júlia, Hordós Adél Zita, Kis 194 Károly, Kis-Tóth Janka, Kovács 111 Bence, Limpek Balázs, Mészáros 916 Márton, Molnár 410 István, Német Franciska, Pásti Bence, Székelyhidi Klára, Szigeti Donát, Wagner Dávid Barnabás. 4 pontot kapott: Ajtai Boglárka, Halász 237 Lajos, Pipis Panna, Sebe Anna, Tóth Benedek, Varga Ákos. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 6 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 4 dolgozat.
A KöMaL 2018. decemberi matematika feladatai

