 |
A C. 1526. feladat (2019. február) |
C. 1526. Egy négyzet körülírt körének az oldalakra vett tükörképeit a négyzet belsejében érintő kör területét jelölje \(\displaystyle T\). Egy tükörképet és a körülírt kört is belülről érintő kör területét jelölje \(\displaystyle t\). Határozzuk meg \(\displaystyle \frac{T}{t}\) lehetséges legkisebb értékét.
(5 pont)
A beküldési határidő 2019. március 11-én LEJÁRT.
Megoldás. Legyen a négyzet oldala 2 (megjegyezzük, hogy az oldal bármennyinek választható, a feladat végeredményét nem befolyásolja, hiszen a területek arányát vizsgáljuk). Ekkor a körülírt körének sugara \(\displaystyle \sqrt{2}\). Először jegyezzük meg, hogy pontosan egy olyan kör létezik, ami a körülírt kör oldalakra vett tükörképeit a négyzet belsejében érinti, legyen ez \(\displaystyle K\), sugara pedig \(\displaystyle R\). Ekkor az ábra jelöléseit használva \(\displaystyle R= ON-2PN= \sqrt{2}-2(\sqrt{2}-1)=2-\sqrt{2}.\)
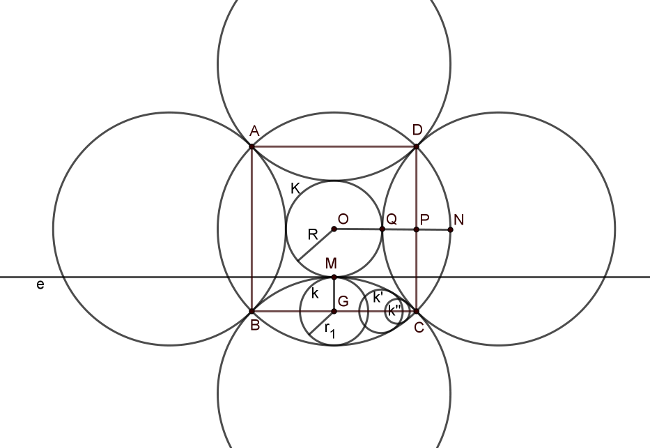
Másrészt olyan körből, ami egy tükörképet és a körülírt kört is belülről érinti végtelen sok van, például az ábrán \(\displaystyle k, k^{'} \text{ és } k^{''}\). Ezek területét jelölje rendre \(\displaystyle t, t^{'} \text{ és } t^{''}\). Ahhoz, hogy \(\displaystyle \frac{T}{t}\) lehetséges legkisebb értékét meghatározzuk, meg kell határozni \(\displaystyle t\) lehető legnagyobb értékét, hiszen \(\displaystyle T\) fix. Megmutatjuk, hogy a \(\displaystyle k\) kör területe a legnagyobb (természetesen szimmetria okokból 4 db ugyanekkora sugarú kör van, mindegyik tükörképhez tartozik egy). Ez pedig az a kör, ami a \(\displaystyle K\) kört ugyanabban az \(\displaystyle M\) pontban érinti, mint a tükörkép kör. Ehhez megmutatjuk, hogy a \(\displaystyle k\) kör sugara (\(\displaystyle r\)) a legnagyobb. Húzzuk be \(\displaystyle k\)-hoz \(\displaystyle M\)-ben az \(\displaystyle e\) érintőt. Ez párhuzamos a négyzet \(\displaystyle BC\) oldalával, valamint a tükörkép körnek is érintője. Mivel az érintőnek pontosan egy közös pontja van a körrel és az összes többi pontja külső pont, így \(\displaystyle e\)-nek nem lesz közös pontja a többi (\(\displaystyle k^{'}, k^{''}, \dots\)) körrel. Továbbá mivel az összes \(\displaystyle k\) kör középpontja \(\displaystyle BC\)-n, a közös húron van, így azok sugara biztosan kisebb \(\displaystyle r\)-nél.
Már csak az van hátra, hogy kiszámoljuk \(\displaystyle r\)-t: \(\displaystyle r=\sqrt{2}-1\). (A sugár értéke éppen \(\displaystyle PN\) hossza, ami \(\displaystyle ON\) és \(\displaystyle OP\) különbségeként megkapható, és értéke \(\displaystyle \sqrt{2}-1\).) Azaz \(\displaystyle \frac{T}{t}\) lehetséges legkisebb értéke
\(\displaystyle \frac{T}{t}=\frac{(2-\sqrt{2})^2 \pi}{(\sqrt{2}-1)^2 \pi}=2.\)
A keresett lehetséges legkisebb érték: \(\displaystyle 2\).
Statisztika:
A KöMaL 2019. februári matematika feladatai
