Problem C. 1529. (February 2019)

C. 1529. Prove that every right-angled triangle can be divided into \(\displaystyle 3k+2\) isosceles triangles where \(\displaystyle k\) is any positive integer.

(5 pont)

Deadline expired on March 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

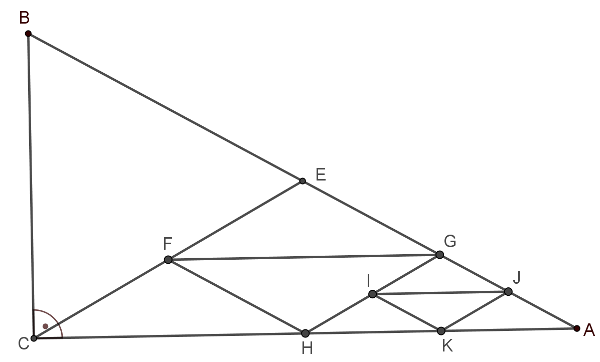
Megoldás. Használjuk az ábra jelöléseit. Először vegyük az \(\displaystyle AB\) átfogó felezőpontját (ami egyben a háromszög köréírt körének középpontja) ez legyen \(\displaystyle E\), majd kössük ezt össze \(\displaystyle C\)-vel. Ekkor az \(\displaystyle ABC\) háromszöget felbontottuk 2 egyenlőszárú háromszögre \(\displaystyle CAE\)-re és \(\displaystyle EBC\)-re (hiszen \(\displaystyle AE=BE=CE\)). Ezután elegendő már ezen egyenlőszárú háromszögek valamelyikét továbbontanunk egyenlőszárú háromszögekre. Válasszuk ki az egyik háromszögünket, például \(\displaystyle CAE\)-t, és húzzuk be a középvonalait. Ekkor 4 db (hozzá hasonló) egyenlőszárú háromszögre bontottuk fel \(\displaystyle CAE\)-t, így a háromszögeink száma 3-mal nőtt. Ezután a lépés után 5 egyenlőszárú háromszögre bontottuk a kiindulási derékszögű háromszögünket. Hasonló módon tetszőleges \(\displaystyle k\) mellett fel tudjuk bontani \(\displaystyle 3k+2\) egyenlőszárú háromszögre, hiszen először a fent említett módon 2-re osztjuk, majd \(\displaystyle k\)-szor ismételjük azt a lépést, hogy kiválasztjuk az egyik felbontásban szereplő egyenlőszárú háromszöget és a középvonalaival 4 kisebb egyenlőszárú háromszögre bontjuk. (Ahogy már említettük, minden ilyen lépésben 3-mal nő a háromszögek száma, így végül \(\displaystyle 3k+2\) lesz.)

Statistics:

169 students sent a solution.
5 points:	129 students.
4 points:	33 students.
3 points:	2 students.
1 point:	1 student.
0 point:	1 student.
Not shown because of missing birth date or parental permission:	3 solutions.

Problems in Mathematics of KöMaL, February 2019