 |
A C. 1531. feladat (2019. február) |
C. 1531. Egy szabályos háromoldalú egyenes hasáb térfogata \(\displaystyle 2~\textrm{dm}^3\). Legalább mekkora a hasáb felszíne?
(5 pont)
A beküldési határidő 2019. március 11-én LEJÁRT.
Megoldás. A hasábunk alap- és fedőlapja egy-egy szabályos háromszög. Legyen ennek az oldala \(\displaystyle a\). Ekkor a háromszög területe: \(\displaystyle \frac{\sqrt{3}}{4}a^2\). A hasáb magassága (azaz az oldallapok egyik oldala) legyen \(\displaystyle m\).
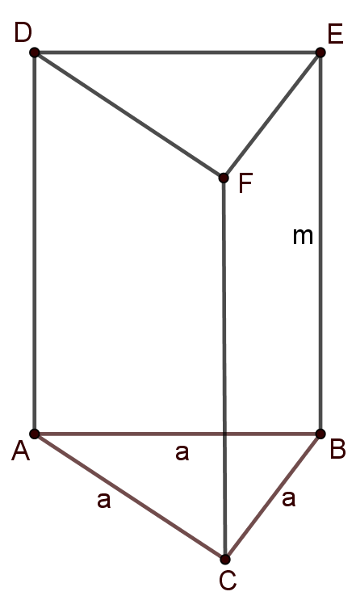
Tudjuk, hogy a hasáb térfogata \(\displaystyle 2\ (\text{dm}^3)\), azaz
\(\displaystyle 2=\frac{\sqrt{3}}{4}a^2 \cdot m .\)
Ebből
\(\displaystyle m= \frac{8}{\sqrt{3}a^2}.\)
Most ezeket az összefüggéseket felhasználva írjuk fel a hasáb felszínét:
\(\displaystyle A=2 \cdot \frac{\sqrt{3}}{4}a^2 + 3 \cdot a \cdot \frac{8}{\sqrt{3}a^2}= \frac{\sqrt{3}}{2}a^2 + \frac{8\sqrt{3}}{a}= \frac{\sqrt{3}}{2} \left(a^2+ \frac{16}{a} \right).\)
Ahhoz, hogy meghatározzuk, hogy legalább mekkora a hasábunk felszíne, meg kell határozni, hogy \(\displaystyle a^2+ \frac{16}{a}\) legalább mekkora. Ehhez a számtani és mértani közepek közti összefüggést írjuk fel a következő három számra: \(\displaystyle a^2, \frac{8}{a}, \frac{8}{a}\).
\(\displaystyle \frac{a^2+ \frac{8}{a}+\frac{8}{a}}{3} \geq 4,\)
azaz
\(\displaystyle a^2+ \frac{16}{a}\geq 12.\)
Ebből
\(\displaystyle A \geq 6\sqrt{3}.\)
Így a hasábunk felszíne legalább \(\displaystyle 6\sqrt{3}\ \text{dm}^2.\)
Megjegyezzük, hogy ez tényleg elő is fordulhat: A felszín akkor lesz \(\displaystyle 6\sqrt{3}\ \text{dm}^2\), ha a számtani-mértani közepek közötti egyenlőtlenség egyenlőséggel teljesül, vagyis, ha \(\displaystyle a^2=8/a\), azaz, \(\displaystyle a=2\). Tehát akkor lesz \(\displaystyle 6\sqrt{3}\ \text{dm}^2\) a felszín, ha a szabályos háromszög oldala \(\displaystyle 2\ \text{dm}\), a hasáb magassága pedig \(\displaystyle \frac{2}{\sqrt{3}} \ \text{dm}\).
Statisztika:
52 dolgozat érkezett. 5 pontot kapott: Ajtai Boglárka, Babolcsay Barbara, Cseke Tibor123, Debreczeni Tibor, Draskóczi Dóra Boglárka, Gál Bence, Gárgyán Barnabás, Gyuricza Gergő, Hordós Adél Zita, Horváth 142 Tamara, Jankovits András, Kalabay László, Kis 194 Károly, Kis-Tóth Janka, Kovács 111 Bence, Kubik Emese, Mészáros 916 Márton, Molnár 410 István, Nyitrai Boglárka, Rozgonyi Gergely, Sal Dávid, Sebe Anna, Székelyhidi Klára, Szigeti Donát, Varga Ákos. 4 pontot kapott: Laczkó Anna, Nyerges Péter, Schäffer Tamás, Szabó 677 Balázs István, Szabó Bence Attila. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 4 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2019. februári matematika feladatai
