 |
A C. 1533. feladat (2019. március) |
C. 1533. Egy derékszögű háromszög kerülete \(\displaystyle k\), egyik befogója \(\displaystyle b\), a vele szemközti szög pedig \(\displaystyle \beta\). Tekintsük azt a háromszöget, amelynek \(\displaystyle 45^\circ\)-os szögének szárain levő oldalainak hossza \(\displaystyle k\) és \(\displaystyle b\cdot\sqrt{2}\,\). Határozzuk meg a legkisebb szögét.
(5 pont)
A beküldési határidő 2019. április 10-én LEJÁRT.
1. megoldás. A feladatban szereplő derékszögű háromszög csúcsai legyenek \(\displaystyle A, B, C\) (a szokásos módon). Az ábrán látható módon a \(\displaystyle BC\) oldalegyenesre mérjünk fel \(\displaystyle c\) hosszú szakaszt \(\displaystyle B\)-ből és \(\displaystyle b\) hosszú szakaszt \(\displaystyle C\)-ből, a szakaszok másik végpontja rendre legyen \(\displaystyle D\) és \(\displaystyle E\).

Ekkor az \(\displaystyle ACE\) háromszög derékszögű és egyenlő szárú, így a másik két szöge \(\displaystyle 45^{\circ}\)-os, az átfogója pedig \(\displaystyle b \sqrt2\) a Pitagorasz-tételből. Másrészt \(\displaystyle DE=k\), azaz az \(\displaystyle ADE\) háromszög pont olyan, hogy a \(\displaystyle 45^\circ\)-os szögének szárain levő oldalainak hossza \(\displaystyle k\) és \(\displaystyle b\cdot\sqrt{2}\). (Ez a három adat egybevágóság erejéig meghatározza már a háromszöget.) Már csak ennek a háromszögnek kell meghatározni a legkisebb szögét. Az \(\displaystyle ADB\) háromszög egyenlő szárú, két alapon fekvő szöge \(\displaystyle \beta/2\), mivel ezek összege egyenlő a harmadik csúcsnál lévő külső szöggel, ami \(\displaystyle \beta\). Az \(\displaystyle ADE\) háromszög \(\displaystyle A\) csúcsnál levő szöge biztosan a legnagyobb, hisz nagyobb, mint \(\displaystyle 45^\circ + \beta/2\), míg a másik két szög \(\displaystyle 45^\circ\), illetve \(\displaystyle \beta/2\). Továbbá mivel \(\displaystyle \beta\) egy derékszögű háromszög nem derékszöge, így \(\displaystyle \beta < 90^{\circ}\), azaz \(\displaystyle \frac{\beta}{2} < 45^{\circ}\).
Tehát a feladatban szereplő háromszög legkisebb szöge \(\displaystyle \frac{\beta}{2}\).
2. megoldás. Először nézzük a derékszögű háromszöget. Legyen a két befogója \(\displaystyle a\) és \(\displaystyle b\). A feladat szövege alapján kerülete \(\displaystyle k\), \(\displaystyle b\)-vel szemközti szöge \(\displaystyle \beta\).
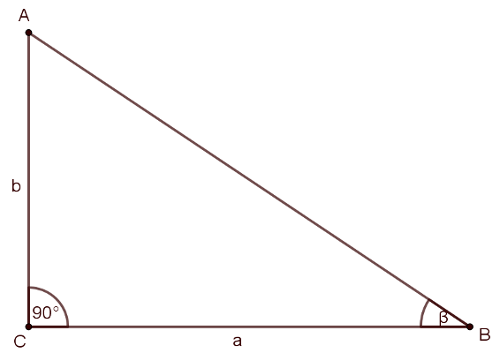
Ekkor \(\displaystyle a= b \ctg \beta\). A kerülete pedig, Pitagorasz-tétel segítségével felírva az átfogót, \(\displaystyle k= b + b \ctg \beta + \sqrt{b^2+ b^2 \ctg^2 \beta}\).
Most nézzük a másik háromszöget.
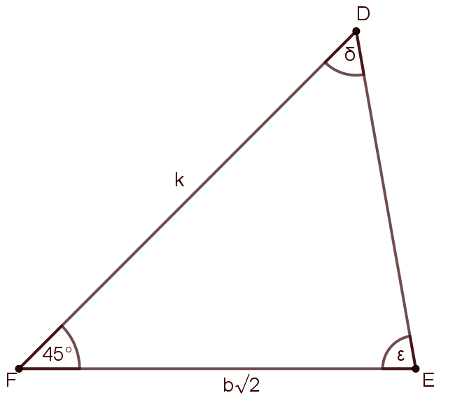
Mivel \(\displaystyle k =a+b+\sqrt{a^2+b^2}> b \sqrt{2}\), ezért \(\displaystyle \epsilon >\delta\), azaz \(\displaystyle \delta \)-t elég meghatározni. Valamint jegyezzük meg, hogy \(\displaystyle \epsilon = 135^{\circ} - \delta\). Most írjuk fel a szinusztételt a \(\displaystyle DEF\) háromszögben:
\(\displaystyle \frac{k}{b \sqrt{2}}=\frac{\sin (135^{\circ} - \delta)}{\sin \delta}.\)
Most \(\displaystyle k\) helyére helyettesítsük be \(\displaystyle k= b + b \ctg \beta + \sqrt{b^2+ b^2 \ctg^2 \beta}\)-t, a jobb oldalon pedig alkalmazzuk a megfelelő addíciós tételt. Valamint jegyezzük meg, hogy a megoldás lépéseiben használni fogjuk, hogy \(\displaystyle \beta, \delta\) háromszög szögei, azaz értékük \(\displaystyle 0^{\circ}\) és \(\displaystyle 180^{\circ}\) közötti:
\(\displaystyle \frac{b + b \ctg \beta + \sqrt{b^2+ b^2 \ctg^2 \beta}}{b \sqrt{2}}=\frac{\sin 135^{\circ} \cos \delta - \cos135^{\circ} \sin \delta} {\sin \delta}.\)
Ezt tovább alakítva
\(\displaystyle \frac{1 + \ctg \beta + \sqrt{1+ \ctg^2 \beta}}{ \sqrt{2}}= \frac{\sqrt2}{2} \cdot \frac{\cos \delta}{\sin \delta} + \frac{\sqrt2}{2} = \frac{1}{\sqrt2} (\ctg \delta + 1).\)
Szorozzuk be mindkét oldalt \(\displaystyle \sqrt 2\)-vel, majd vonjunk ki 1-et:
\(\displaystyle \ctg \beta + \sqrt{1+ {\ctg}^{2} \beta} = \ctg \delta.\)
Felhasználva, hogy \(\displaystyle \sin^2\beta+\cos^2\beta=1\):
\(\displaystyle \ctg \beta + \sqrt{\frac{1} {{\sin}^{2} \beta}} = \ctg \delta,\)
majd alakítsuk tovább a bal oldalt, felhasználva, hogy \(\displaystyle \sin \beta >0\) (háromszög szögéről lévén szó):
\(\displaystyle \frac{\cos \beta+1}{\sin \beta} = \ctg \delta,\)
amiből a \(\displaystyle \sin\) és \(\displaystyle \cos\) addíciós tételét használva:
\(\displaystyle \frac{2 \cos^2 \frac{\beta}{2}}{2 \sin \frac{\beta}{2} \cos \frac{\beta}{2} } = \ctg \delta.\)
Ezt egyszerűsítve kapjuk, hogy
\(\displaystyle \ctg \frac{\beta}{2} = \ctg \delta.\)
Továbbá \(\displaystyle \beta\) és \(\displaystyle \delta\) háromszög szögei, így
\(\displaystyle \frac{\beta}{2}=\delta.\)
Mivel \(\displaystyle \beta\) egy derékszögű háromszög nem derékszöge, így \(\displaystyle \beta < 90^{\circ}\), azaz \(\displaystyle \frac{\beta}{2} < 45^{\circ}\).
Tehát a feladatban szereplő háromszög legkisebb szöge \(\displaystyle \frac{\beta}{2}\).
Statisztika:
A KöMaL 2019. márciusi matematika feladatai
