 |
A C. 1539. feladat (2019. április) |
C. 1539. Az \(\displaystyle ABCD\) négyzet \(\displaystyle AB\) oldalának \(\displaystyle A\)-hoz közelebbi negyedelőpontját jelölje \(\displaystyle E\), \(\displaystyle F\) pedig legyen a \(\displaystyle BD\) átló tetszőleges pontja. Határozzuk meg az \(\displaystyle AF+EF\) összeg minimumát.
(5 pont)
A beküldési határidő 2019. május 10-én LEJÁRT.
Megoldás. Vegyük a négyzet oldalát egységnyinek: \(\displaystyle AB=1\).
Először tükrözzük az \(\displaystyle E\) pontot a négyzet \(\displaystyle BD\) átlójára, képe legyen \(\displaystyle E'\). Ekkor \(\displaystyle E'\) rajta lesz a \(\displaystyle BC\) oldalon (a \(\displaystyle C\)-hez közelebbi negyedelőpont lesz) és \(\displaystyle FE=FE'\) (a tengelyes tükrözés tulajdonságai miatt), azaz a feledattal ekvivalens \(\displaystyle AF+E'F\) összeg minimumát keresni.
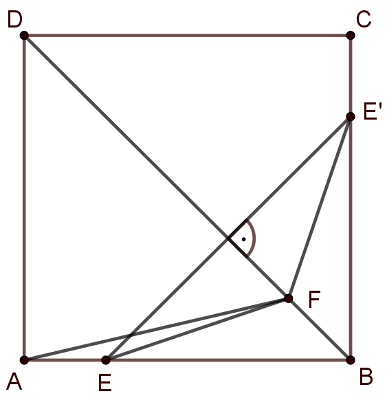
Így az \(\displaystyle AFE'\) töröttvonal hosszának minimumát keressük, és ez a töröttvonal akkor a legrövidebb, ha egyenes (a háromszög-egyenlőtlenség miatt), azaz az \(\displaystyle A\), \(\displaystyle F\) és \(\displaystyle E'\) pontoknak egy egyenesen kell lennie. Ezek alapján a legjobb \(\displaystyle F\) nem más, mint \(\displaystyle AE'\)-nek és \(\displaystyle BD\)-nek a metszéspontja (lásd a következő ábrán).
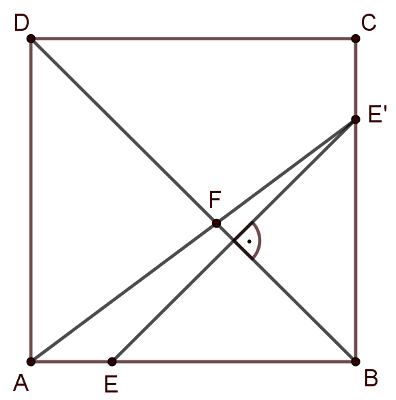
Ekkor a keresett \(\displaystyle AF+E'F\) minimuma nem más mint az \(\displaystyle AE'\) szakasz hossza. Ennek meghatározásához írjuk fel a Pitagorasz-tételt az \(\displaystyle ABE'\) háromszögre:
\(\displaystyle AE'= \sqrt{1+\left(\frac{3}{4}\right)^2}=\frac{5}{4}.\)
Azaz az \(\displaystyle AF+EF\) összeg minimuma \(\displaystyle \frac{5}{4}\).
Statisztika:
104 dolgozat érkezett. 5 pontot kapott: 56 versenyző. 4 pontot kapott: 10 versenyző. 3 pontot kapott: 13 versenyző. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 10 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2019. áprilisi matematika feladatai

