A C. 1564. feladat (2019. október)

C. 1564. Egy \(\displaystyle 6 \times 6\)-os négyzetrácsot rácsvonalak mentén \(\displaystyle n\) darab különböző területű téglalapra bontottunk föl. Adjunk példát a fölbontásra minden lehetséges \(\displaystyle n>1\) érték esetén.

(5 pont)

A beküldési határidő 2019. november 11-én LEJÁRT.

Megoldás. Először vegyük észre, hogy 8 darabnál több téglalapra nem bonthattuk fel. Mivel minden téglalapnak különböző területűnek kellene lennie, így a területük összege legalább az első \(\displaystyle n\) pozitív egész szám összege lenne, és ez már \(\displaystyle n=9\)-re is több, mint 36. Most nézzük meg, hogy 8-ra fel tudjuk-e bontani: a számok összege 1-től 8-ig éppen 36, azaz csak úgy lenne lehetséges, ha a téglalapok területe éppen \(\displaystyle 1,2, \dots, 8\) lenne. Azonban a 7 prím, azaz 7 területű téglalap csak 1 és 7 oldalhosszakkal fordulhat elő, ami ,,nem fér bele'' egy \(\displaystyle 6\times 6\)-os négyzetbe. Így ez sem lehetséges.

Másrészről pedig, \(\displaystyle 2,3, \dots, 7\) darab különböző területű téglalapra már felbontható. Az ábrán egy-egy példa látható jó felbontásra:

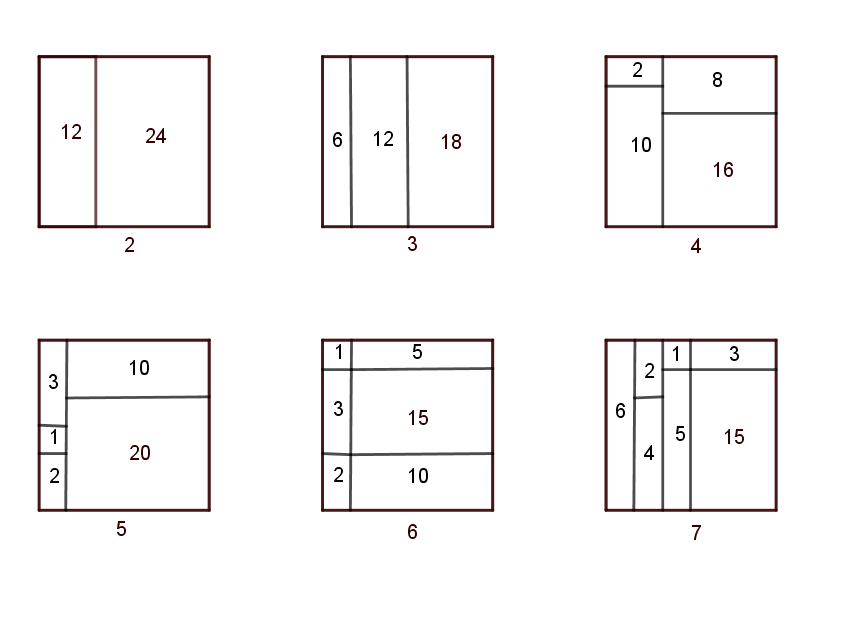
Statisztika:

273 dolgozat érkezett.
5 pontot kapott:	212 versenyző.
4 pontot kapott:	14 versenyző.
3 pontot kapott:	20 versenyző.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	13 versenyző.

A KöMaL 2019. októberi matematika feladatai