Problem C. 1582. (January 2020)

C. 1582. Let \(\displaystyle ABP\), \(\displaystyle BCQ\), \(\displaystyle CDR\), \(\displaystyle DAS\) denote the regular triangles drawn on the sides of paralellogram \(\displaystyle ABCD\) on the outside. What requirements does the parallelogram need to meet in order for \(\displaystyle PQRS\) to be a square?

(5 pont)

Deadline expired on February 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit.

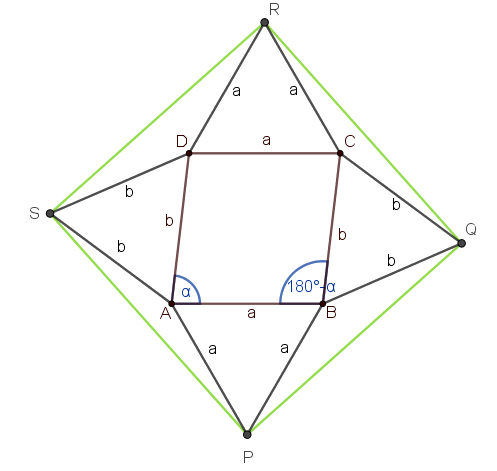
Ha \(\displaystyle PQRS\) négyzet, akkor \(\displaystyle PQB\triangle\cong RQC\triangle\cong RSD\triangle\cong PSA\triangle\), hiszen oldalaik páronként megegyeznek.

Először tegyük fel, hogy a \(\displaystyle PQRS\) négyszög egyik oldala sem metsz bele semelyik szabályos háromszögbe sem, vagyis az ábra valóban így néz ki.

Ekkor \(\displaystyle SRD\angle+60^{\circ}+QRC\angle=90^{\circ}\), és így a négy egybevágó háromszög szögeinek egyenlőségéből \(\displaystyle SRD\angle=QRC\angle=15^{\circ}\). Hasonlóan látható be, hogy \(\displaystyle RSD\angle=PSA\angle=15^{\circ}\). Így az \(\displaystyle SDR\) háromszög (és így a vele egybevágó másik három háromszög) szögei \(\displaystyle 15^{\circ}\), \(\displaystyle 15^{\circ}\) és \(\displaystyle 180^{\circ}-2\cdot15^{\circ}=150^{\circ}\). Ebből egyrészt következik, hogy ezek a háromszögek egyenlő szárúak, tehát \(\displaystyle a=b\), másrészt pedig \(\displaystyle CDA\angle=DAB\angle=ABC\angle=BCD\angle=360^{\circ}-(150^{\circ}+2\cdot60^{\circ})=90^{\circ}\). Tehát az \(\displaystyle ABCD\) négyszög oldalai egyenlőek, szögei derékszögek, vagyis négyzet.

Most tegyük fel, hogy a \(\displaystyle PQRS\) négyzet valamelyik oldala belemetsz két szomszédos szabályos háromszögbe (vagy esetleg egybeesik egy-egy oldalukkal). Legyen ez pl. a \(\displaystyle PS\) szakasz. Ekkor a \(\displaystyle PAS\) szög kisebb vagy egyenlő \(\displaystyle 180^{\circ}\)-nál és három szög összegeként áll elő: \(\displaystyle PAS\angle=PAB\angle+BAD\angle+DAS\angle=120^{\circ}+\alpha\), tehát \(\displaystyle \alpha\leq60^{\circ}\). Ekkor \(\displaystyle ABC\angle=180^{\circ}-\alpha\geq120^{\circ}>60^{\circ}\) és így a \(\displaystyle PQ\) szakasz nem metsz bele a szabályos háromszögekbe. Ugyanakkor a fenti négy háromszög egybevágóságából \(\displaystyle 120^{\circ}+\alpha=PAS\angle=PBQ\angle=360^{\circ}-(60^{\circ}+(180^{\circ}-\alpha)+ 60^{\circ})=60^{\circ}+\alpha\), ami ellentmondás. Tehát ez nem lehetséges.

Másrészt, ha \(\displaystyle ABCD\) négyzet, akkor a \(\displaystyle 90^{\circ}\)-os forgásszimmetria alapján \(\displaystyle PQRS\) ia négyzet.

Tehát ahhoz, hogy \(\displaystyle PQRS\) négyzet legyen, az \(\displaystyle ABCD\) négyszögnek is négyzetnek kell lennie.

Statistics:

122 students sent a solution.
5 points:	Cserkuti Sándor, Csilling Dániel, Dózsa Levente, Egyházi Hanna, Feczkó Nóra, Fekete Patrik, Foris Dávid, Horváth Milán, Kalocsai Zoltán, Károly Kinga, Kurucz Márton, Mátéfy Ádám , Németh László Csaba, Németh Máté Előd, Sárvári Borka Luca, Schneider Dávid, Szabó Réka, Szabó Zóra.
4 points:	38 students.
3 points:	25 students.
2 points:	15 students.
1 point:	10 students.
0 point:	15 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, January 2020