Problem C. 1586. (January 2020)

C. 1586. The points \(\displaystyle D\) and \(\displaystyle E\) divide side \(\displaystyle AB\) of triangle \(\displaystyle ABC\) into three equal parts. Let \(\displaystyle P\) be an arbitrary interior point of line segment \(\displaystyle DE\). Draw parallels to line \(\displaystyle PC\) through the points \(\displaystyle D\) and \(\displaystyle E\). These lines intersect sides \(\displaystyle AC\) and \(\displaystyle BC\) at points \(\displaystyle Q\) and \(\displaystyle R\), respectively. Show that the area of quadrilateral \(\displaystyle PRCQ\) equals the area of triangle \(\displaystyle APQ\).

Proposed by B. Bíró, Eger

(5 pont)

Deadline expired on February 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

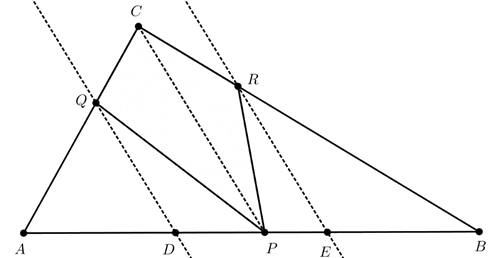
Az ábrán látható módon kössük össze \(\displaystyle Q\)-t és \(\displaystyle R\)-t \(\displaystyle P\)-vel.

A \(\displaystyle CD\) és \(\displaystyle CE\) egyenesek a háromszöget három egyenlő területű részre osztják, mert az \(\displaystyle ADC\), \(\displaystyle DEC\) és \(\displaystyle EBC\) háromszögeknek a \(\displaystyle C\) csúcshoz tartozó magassága közös, és az \(\displaystyle AD\), \(\displaystyle DE\), \(\displaystyle EB\) alapok egyenlő hosszúak.

A \(\displaystyle PCQ\) háromszög területe egyenlő a \(\displaystyle PCD\) háromszög területével, hiszen a két háromszögnek a \(\displaystyle PC\) oldalhoz tartozó magassága \(\displaystyle PC\) és \(\displaystyle DQ\) párhuzamossága miatt egyenlő.

Hasonlóan láthatjuk be, hogy a \(\displaystyle PCR\) háromszög területe egyenlő a \(\displaystyle PCE\) háromszög területével. Ez pedig azt jelenti, hogy

\(\displaystyle T_{PRCQ}=T_{PCQ}+T_{PCR}=T_{PCD}+T_{PCE}=T_{DEC}=T_{ABC}/3.\)

Megmutatjuk, hogy \(\displaystyle T_{APQ}\) is harmadrésze az \(\displaystyle ABC\) háromszög területének. Ugyancsak \(\displaystyle PC\) és \(\displaystyle DQ\) párhuzamossága miatt a \(\displaystyle DCQ\) és \(\displaystyle DPQ\) háromszögek területe egyenlő, ezért

\(\displaystyle T_{ABC}/3=T_{ADC}=T_{DCQ}+T_{ADQ}=T_{DPQ}+T_{ADQ}=T_{APQ}.\)

Beláttuk, hogy az \(\displaystyle APQ\) háromszög területe is az \(\displaystyle ABC\) háromszög területének harmadrésze.

Tehát a \(\displaystyle PRCQ\) négyszög területe valóban egyenlő az \(\displaystyle APQ\) háromszög területével.

Statistics:

27 students sent a solution.
5 points:	Féger Tamás, Hajdú Bálint, Kadem Aziz, Kalabay László, Kis 194 Károly, Molnár Réka, Sümegi Géza.
4 points:	Andó Lujza, Biró 424 Ádám, Fekete András Albert, Kelemen Anna, Lakatos Enikő, Ludányi Levente, Molnár Kristóf András, Palencsár Enikő, Schneider Anna, Szabó Csege, Szigeti Donát, Zaránd Andris.
3 points:	3 students.
2 points:	1 student.
1 point:	3 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, January 2020