 |
A C. 1617. feladat (2020. szeptember) |
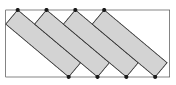
C. 1617. Elhelyezhető-e átfedés nélkül négy darab \(\displaystyle 2\times 8\)-as téglalap egy \(\displaystyle 7\times15\)-ös téglalap belsejében az ábrán látható elrendezésben? (Az ábra nem arányos.)
(5 pont)
A beküldési határidő 2020. október 12-én LEJÁRT.
Megoldás. Helyezzük el a keskeny téglalapokat a nagy téglalapon úgy, hogy két-két csúcsuk illeszkedjen a nagy téglalap hosszabbik oldalaira, a bal szélső egyik csúcsa pedig a nagy téglalap rövidebb oldalára. Vizsgáljuk meg a le nem fedett részeket.

Az ábrán jelölt szögek megegyező nagyságúak (\(\displaystyle AFP\sphericalangle\) és \(\displaystyle BPE\sphericalangle\) merőleges szárú szögek, \(\displaystyle AFP\sphericalangle\) és \(\displaystyle GEH\sphericalangle\) váltószögek), így \(\displaystyle AFP\triangle \sim BPE\triangle\). Az átfogók aránya miatt \(\displaystyle BPE\)-t a negyedére kicsinyítettük: ha a \(\displaystyle BE\) távolságot \(\displaystyle x\)-szel jelöljük, akkor \(\displaystyle AP=\frac{x}{4}\). Ebből az következik, hogy \(\displaystyle PB=7-\frac{x}{4}\). Az \(\displaystyle AF=y\)-t szintén kifejezhetjük a kicsinyítés segítségével: \(\displaystyle \displaystyle{y=\frac{7-\frac{x}{4}}{4}}=\frac{28-x}{16}\).
A \(\displaystyle BPE\triangle\) és \(\displaystyle GEH\triangle\) hasonlósága miatt meg tudjuk határozni az \(\displaystyle EH=z\) szakasz hosszát a megfelelő oldalpárok arányának egyenlőségéből: \(\displaystyle \displaystyle{\frac{2}{z}=\frac{7-\frac{x}{4}}{8}}\), ahonnan \(\displaystyle \displaystyle{z=\frac{16}{7-\frac{x}{4}}=\frac{64}{28-x}}\).
\(\displaystyle BPE\) derékszögű háromszögben a Pitagorasz-tétel felírásával meghatározható \(\displaystyle x\) pontos értéke: \(\displaystyle \displaystyle{\left(7-\frac{x}{4}\right)^2+x^2=8^2}\). A műveletek elvégzése után megoldandó a \(\displaystyle 17x^2-56x-240=0\) egyenlet. Mivel \(\displaystyle x>0\), ezért a kapott két gyök közül a pozitív lesz a megoldás: \(\displaystyle x=\frac{28+\sqrt{4864}}{17}\). Ezzel \(\displaystyle 5,749<x<5,75\), \(\displaystyle z>\frac{64}{28-5,749}>2,876\) és \(\displaystyle y>\frac{28-5,75}{16}>1,39\). A 4 keskeny téglalap elhelyezéséhez szükséges szélesség a \(\displaystyle BE\) szakasz hossza, hozzá kell adni a \(\displaystyle GEH\) háromszög \(\displaystyle EH\) átfogójának hosszát háromszor, hiszen a háromszög még kétszer szerepel elcsúsztatva; végül az \(\displaystyle AFP\) háromszöggel egybevágó háromszög \(\displaystyle AF\)-fel megegyező befogójának hosszát. A keresett szélesség tehát: \(\displaystyle x+3z+y> 5,749+3\cdot 2,876+1,39=15,767>15\).
A feladat szerinti elrendezésben nem helyezhetőek el a keskeny téglalapok.
Statisztika:
105 dolgozat érkezett. 5 pontot kapott: Baranyi 13 Barnabás, Besze Zsolt, Bettesch Helga Adél, Biborka Dániel, Deák Gergely, Fekete Patrik, Gecseg Bence, Győrffy Nándor, Hajós Balázs, Halász Henrik, Horváth Milán, Kádár 1115 Júlia, Kovács Benedek Noel, Kurucz Márton, Lőw László, Molnár Kristóf, Morvai Eliza, Murai Dóra Eszter, Nagy Dániel, Patricia Janecsko, Pekk Márton, Rózsa Félix, Schleier Anna , Schmercz Blanka, Schneider Dávid, Sipeki Márton, Slézia Dávid, Szabó 423 Ágnes, Szabó Viktória, Szabó Zóra, Szaló Tamás Botond, Szilágyi Kornél Csaba, Szirtes Hanna, Tomesz László Gergő, Tóth Gréta, Van Rijs Dóra, Vankó Lóránt Albert, Vitálos Tünde, Werner Kinga, Wrana Gergő. 4 pontot kapott: 21 versenyző. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 14 versenyző. 0 pontot kapott: 16 versenyző.
A KöMaL 2020. szeptemberi matematika feladatai

