Problem C. 1619. (September 2020)

C. 1619. From the midpoint of each side of an acute-angled triangle, drop perpendiculars to the other two sides. Prove that the area of the hexagon formed by the perpendiculars is half the area of the triangle.

(Croatian problem)

(5 pont)

Deadline expired on October 12, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit! Az \(\displaystyle ABC\) hegyesszögű háromszög oldalfelezőpontjai tehát \(\displaystyle D,E,F\), az ezekből indított merőlegesek talppontjai pedig (az ábra szerint) \(\displaystyle P,Q,R,S,T,U\).

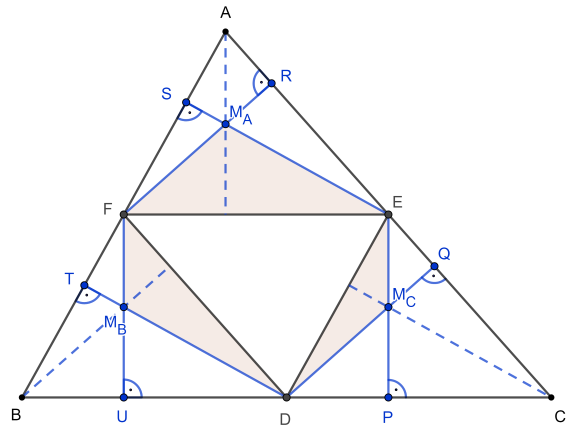
A háromszöget a középvonalai négy egybevágó háromszögre osztják, melyek hasonlók \(\displaystyle ABC\)-hez:
\(\displaystyle AFE,\ FBD,\ EDC,\ DEF\). Ezeknek a háromszögeknek \(\displaystyle 2-2\) magasságát húztuk be, ezek talppontjai a megfelelői oldalak belső pontjai, hiszen a háromszögek hegyesszögűek. Mindhárom háromszögben húzzuk be a harmadik magasságvonalat is, és jelöljük a magasságpontokat \(\displaystyle M_A,M_B,M_C\)-vel. A kérdéses hatszög \(\displaystyle DM_CEM_AFM_B\).

Az \(\displaystyle AFE,\ FBD,\ EDC\) háromszögek egybevágósága alapján világos, hogy \(\displaystyle AFM_A\) és \(\displaystyle EDM_C\) egybevágók, valamint \(\displaystyle AM_AE\) és \(\displaystyle FM_BD\) is egybevágók. Így \(\displaystyle T_{M_AFE}+T_{FM_BD}+T_{EDM_C}=T_{M_AFE}+T_{AM_AE}+T_{AFM_A}=T_{AFE}=\frac{1}{4} T_{ABC}.\) Ez alapján pedig

\(\displaystyle T_{DM_CEM_AFM_B}=T_{M_AFE}+T_{FM_BD}+T_{EDM_C}+T_{DEF}=\frac{1}{4} T_{ABC}+\frac{1}{4} T_{ABC}=\frac{1}{2} T_{ABC}.\)

Ezzel megmutattuk, hogy a kérdéses hatszög területe a háromszög területének felével egyenlő.

Statistics:

185 students sent a solution.
5 points:	71 students.
4 points:	40 students.
3 points:	25 students.
2 points:	16 students.
1 point:	21 students.
0 point:	11 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, September 2020