 |
A C. 1631. feladat (2020. november) |
C. 1631. Egy egységsugarú körön adott az \(\displaystyle AB\) húr. Erre két derékszögű háromszöget emelünk: \(\displaystyle ABC\)-t úgy, hogy \(\displaystyle C\) csúcsa a körön helyezkedik el és \(\displaystyle B\)-nél van a derékszög, az \(\displaystyle ABD\) háromszöget pedig úgy, hogy \(\displaystyle AB\) az átfogója, és egyenlő szárú. Mekkora az \(\displaystyle AB\) húr hossza, ha a két háromszög területe megegyezik? Mekkora ez a terület?
(5 pont)
A beküldési határidő 2020. december 10-én LEJÁRT.
Megoldás. Jelöléseink az ábrán láthatók.
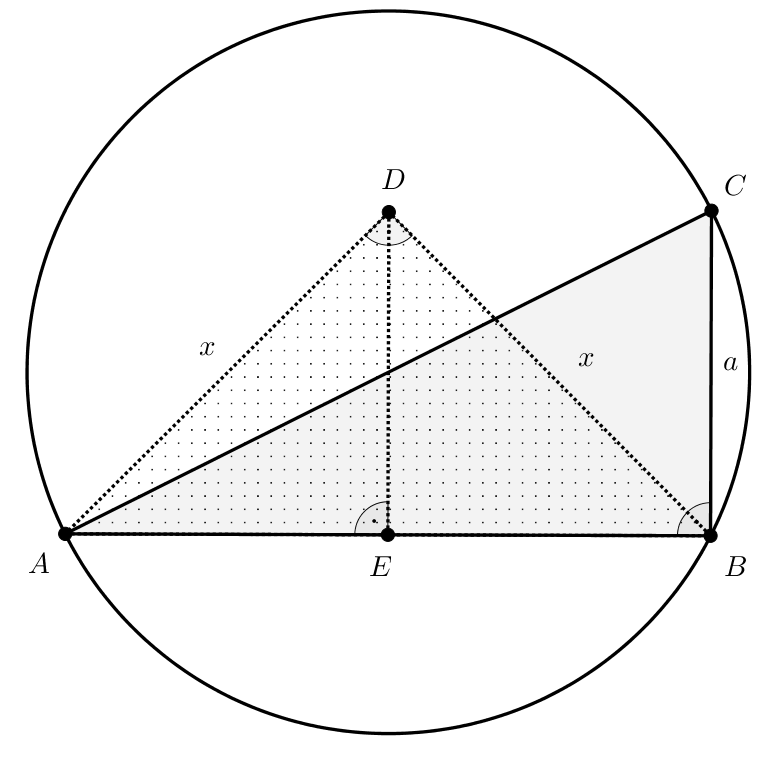
Mivel \(\displaystyle ABC\sphericalangle=90^{\circ}\), ezért \(\displaystyle AC\) az \(\displaystyle ABC\) háromszög körülírt körének átmérője, és így \(\displaystyle AC=2\).
Az \(\displaystyle AD=BD=x\) jelöléssel azt kapjuk, hogy \(\displaystyle AB=x\cdot\sqrt{2}\), és így az ábra \(\displaystyle DE\) szakaszára
\(\displaystyle DE=\frac{x\cdot\sqrt{2}}2\).
A feltétel miatt az \(\displaystyle ABC\) és \(\displaystyle ABD\) háromszögek kétszeres területe is egyenlő, tehát \(\displaystyle a\cdot{AB}=x^2\), azaz \(\displaystyle a\cdot x\cdot \sqrt{2}=x^2\), ahonnan
| \(\displaystyle (1)\) | \(\displaystyle a=\frac{x}{\sqrt{2}}=\frac{x\cdot\sqrt{2}}2.\) |
Felírjuk a Pitagorasz-tételt az \(\displaystyle ABC\) háromszögre:
\(\displaystyle AB^2+BC^2=CA^2\), vagyis \(\displaystyle (x\cdot\sqrt{2})^2+a^2=2^2\). A műveletek elvégzésével és (1) felhasználásával:
| \(\displaystyle (2)\) | \(\displaystyle x=\frac{4}{\sqrt{10}}.\) |
Tudjuk, hogy \(\displaystyle AB=x\cdot\sqrt{2}\), ezért (2) szerint \(\displaystyle AB=\frac{4}{\sqrt{5}}.\)
Az \(\displaystyle ABC\) és \(\displaystyle ABD\) háromszögek területe tehát:
\(\displaystyle T_{ABC}=T_{ABD}=\frac{AB\cdot{a}}2=\frac{x^2}2=0,8.\)
Megjegyzések.
1. A megoldás nyilván nem függ attól, hogy a \(\displaystyle C\) és \(\displaystyle D\) pontokat az \(\displaystyle AB\) egyenes ugyanazon oldalán vettük fel.
2. A megoldásból kiderül, hogy \(\displaystyle BC=DE\), és könnyen bizonyítható, hogy \(\displaystyle CA\) felezi a \(\displaystyle DE\) szakaszt.
Statisztika:
164 dolgozat érkezett. 5 pontot kapott: 72 versenyző. 4 pontot kapott: 30 versenyző. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 16 versenyző. 0 pontot kapott: 8 versenyző. Nem versenyszerű: 17 dolgozat.
A KöMaL 2020. novemberi matematika feladatai

