 |
A C. 1673. feladat (2021. május) |
C. 1673. Egy trapézt átlói négy háromszögre bontanak. A trapéz alapjain fekvő háromszögek területének összege a trapéz területének \(\displaystyle \frac{13}{18}\) része. Mekkora lehet a trapéz másik alapja, ha az egyik 5 cm hosszú?
(5 pont)
A beküldési határidő 2021. június 10-én LEJÁRT.
Megoldás. Ha egy trapéz alapjai egyenlő hosszúak, akkor a trapéz paralelogramma. Egy paralelogrammát az átlói négy egyenlő területű háromszögre bontanak fel, így ekkor a két, alapon fekvő háromszög területének összege a trapéz (paralelogramma) területének a fele lenne. Ez tehát nem lehetséges.
Legyen tehát az \(\displaystyle ABCD\) trapéz \(\displaystyle AB\) és \(\displaystyle CD\) alapjainak hossza \(\displaystyle a\) és \(\displaystyle c\), ahol \(\displaystyle a>c\). További jelöléseink a következő ábrán láthatók.
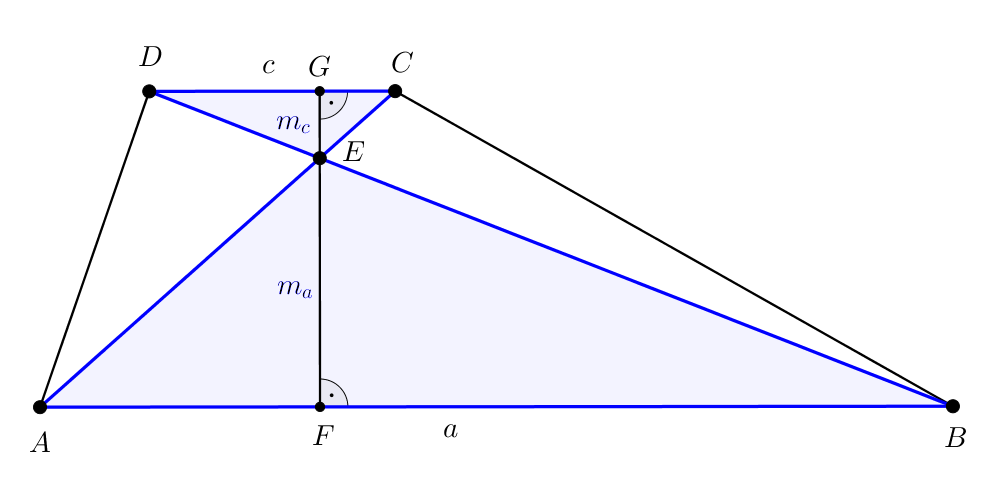
A továbbiakban az \(\displaystyle \frac{a}{c}\) arány megállapítására törekszünk, és attól függ majd a másik alap értéke, hogy a rövidebbik, vagy a hosszabbik alap hossza 5 cm. Mivel \(\displaystyle a>c\), így \(\displaystyle \frac{a}{c}>1\).
Az \(\displaystyle AB\), illetve \(\displaystyle CD\) alapokon fekvő \(\displaystyle ABE\) és \(\displaystyle CDE\) háromszögek területe az ábra jelöléseivel:
| \(\displaystyle (1)\) | \(\displaystyle T_{ABE}=\frac{a\cdot{m_{a}}}{2};\qquad{T_{CDE}=\frac{c\cdot{m_{c}}}{2}},\) |
az \(\displaystyle ABCD\) trapéz területe pedig:
| \(\displaystyle (2)\) | \(\displaystyle T_{ABCD}=\frac{(a+c)\cdot(m_{a}+m_{c})}{2}.\) |
A feladat feltétele szerint
\(\displaystyle T_{ABE}+T_{CDE}=\frac{13}{18}\cdot{T_{ABCD}},\)
ezért (1) és (2) alapján
| \(\displaystyle (3)\) | \(\displaystyle \frac{a\cdot{m_a}}{2}+\frac{c\cdot{m_c}}{2}={\frac{13}{18}}\cdot{\frac{(a+c)\cdot(m_a+m_c)}{2}}.\) |
A műveletek elvégzése és rendezés után (3)-ból azt kapjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle 5a\cdot{m_a}+5c\cdot{m_c}=13c\cdot{m_a}+13a\cdot{m_c}.\) |
A (4) egyenlet mindkét oldalát osztva a nyilván pozitív \(\displaystyle m_c\) számmal:
| \(\displaystyle (5)\) | \(\displaystyle 5a\cdot{\frac{m_a}{m_c}}+5c=13c\cdot{\frac{m_a}{m_c}}+13a.\) |
A trapéz \(\displaystyle AB\) és \(\displaystyle CD\) alapjai párhuzamosak, ezért a megfelelő szögek egyenlősége miatt az \(\displaystyle ABE\) és \(\displaystyle CDE\) háromszögek hasonlók, a hasonlóság aránya \(\displaystyle \frac{a}{c}\)-vel egyenlő. A két hasonló háromszögben a megfelelő oldalakhoz tartozó magasságok aránya megegyezik a hasonlóság arányával, azaz
\(\displaystyle \frac{m_a}{m_c}=\frac{a}{c}.\)
Eszerint az (5) egyenletből először
\(\displaystyle 5\cdot{\frac{a^2}{c}}+5c=26a,\)
majd – mivel az \(\displaystyle \frac ac\) arányt szeretnénk megkapni – \(\displaystyle a\)-val való osztással:
\(\displaystyle 5\cdot{\frac{a}{c}}+5\cdot{\frac{c}{a}}=26.\)
Az \(\displaystyle x=\frac{a}{c}\) jelölést választva, a kapott egyenletből rendezés után az
\(\displaystyle 5x^2-26x+5=0\)
egyenlet adódik. A másodfokú egyenlet gyökei:
\(\displaystyle x_1=5;\qquad{x_2=\frac{1}{5}}.\)
Mivel \(\displaystyle a>c\), ebből \(\displaystyle \frac ac=5\) következik, vagyis ha \(\displaystyle a=5\), akkor \(\displaystyle c=1\), ha pedig \(\displaystyle c=5\), akkor \(\displaystyle a=25\).
Tehát, ha a trapéz egyik alapja 5 cm-es, akkor a másik alap 1 cm, vagy 25 cm hosszúságú.
Statisztika:
A KöMaL 2021. májusi matematika feladatai

