A C. 1684. feladat (2021. október)

C. 1684. Igazoljuk, hogy nincs olyan ötszög, amelynek minden oldala egyenlő hosszúságú és van két $\displaystyle 60^{\circ}$-os szöge.

(5 pont)

A beküldési határidő 2021. november 10-én LEJÁRT.

Megoldás. Indirekt módon bizonyítunk, azaz feltesszük, hogy létezik olyan ötszög, amelynek oldalai egyenlő hosszúak és van két $\displaystyle 60^{\circ}$-os szöge.

Jelöljük az ötszög csúcsait pozitív körüljárási irány szerint haladva az $\displaystyle A, B, C, D, E$ betűkkel, az oldalak hosszúságát $\displaystyle a$-val.

A két $\displaystyle 60^{\circ}$-os szög csúcsai kétféleképpen helyezkedhetnek el: vagy van az ötszögnek olyan oldala, amelynek végpontjai a két $\displaystyle 60^{\circ}$-os szög csúcsai, vagy nincs ilyen oldala az ötszögnek.

Az első esetben feltehető, hogy a kérdéses oldal az $\displaystyle AB=a$ szakasz. Ekkor az $\displaystyle A$, illetve $\displaystyle B$ csúcsokból induló két ötszögoldal másik végpontja $\displaystyle E$, illetve $\displaystyle C$, és nyilvánvaló, hogy ez a két pont különböző. Ilyen feltételek mellett az $\displaystyle ABE$ és az $\displaystyle ABC$ háromszögek szabályos háromszögek, hiszen az $\displaystyle AB=a$ oldalon mindkét háromszögben két $\displaystyle 60^{\circ}$-os fekszik, így a két háromszög harmadik szögei is $\displaystyle 60^{\circ}$-osak.

Ez azonban azt jelenti, hogy az $\displaystyle E$ és $\displaystyle C$ pontok azonosak, így ez az eset nyilván nem lehetséges (1. ábra).

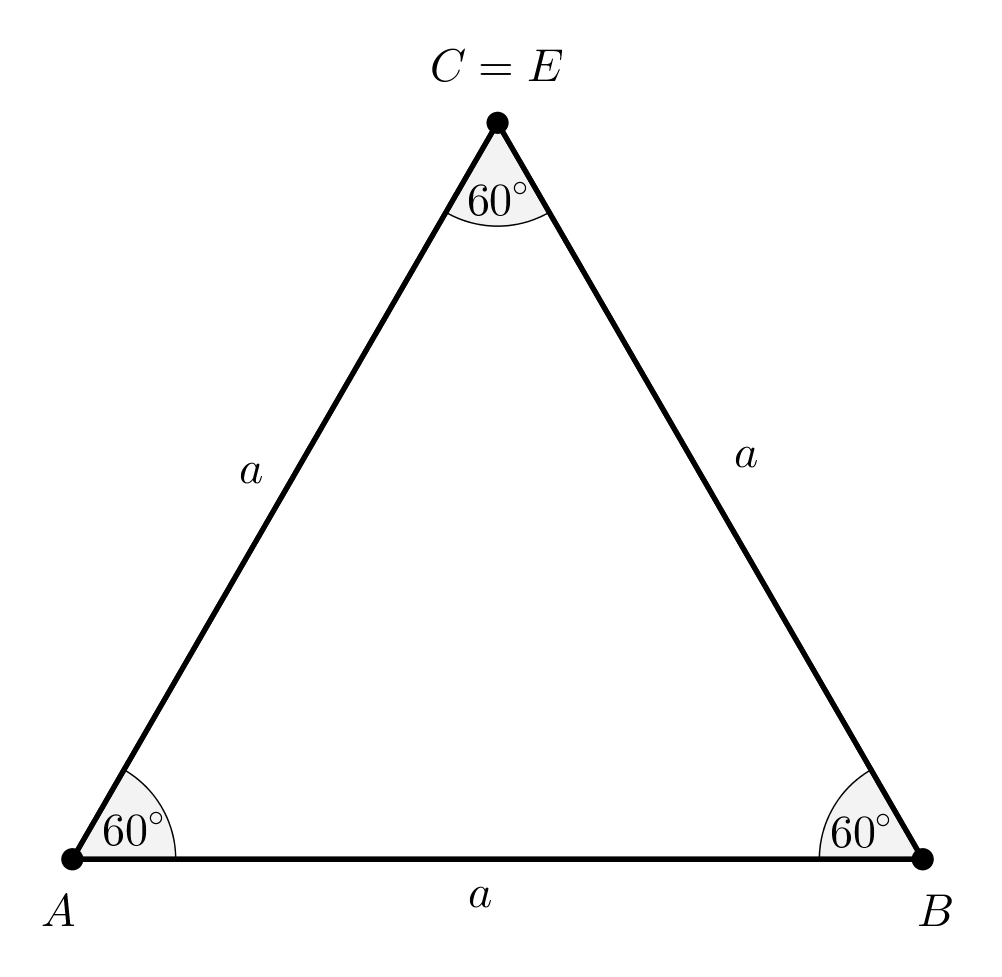
1. ábra

Ha nincs az ötszög oldalai között olyan, amelynek mindkét végpontja a két $\displaystyle 60^{\circ}$-os szög csúcsaival azonos, akkor az általánosság sérelme nélkül feltehetjük, hogy a két szög csúcsai $\displaystyle A$ és $\displaystyle C$.

Az ötszög oldalai egyenlő hosszúak, $\displaystyle AB=AE=a$, továbbá $\displaystyle EAB\sphericalangle=60^{\circ}$, emiatt a $\displaystyle EAB$ háromszög szabályos, hiszen a $\displaystyle B$ és $\displaystyle E$ csúcsoknál fekvő szögei egyenlők, mindkettő $\displaystyle 60^{\circ}$-os. Ezért $\displaystyle BE=a$ is igaz.

Mivel $\displaystyle BC=CD=a$ és $\displaystyle BCD\sphericalangle=60^{\circ}$, ezért az előzőekhez hasonlóan kapjuk, hogy a $\displaystyle BCD$ háromszög is szabályos, és így $\displaystyle BD=a$. Eszerint a $\displaystyle BDE$ háromszögben $\displaystyle BD=BE=a$, de az ötszög oldalainak egyenlősége miatt $\displaystyle DE=a$ is fennáll, ez pedig azt jelenti, hogy a $\displaystyle BDE$ háromszög is szabályos, tehát $\displaystyle EBD\sphericalangle=60^{\circ}$.

Ekkor azonban az $\displaystyle ABCDE$ ötszögben a $\displaystyle B$ csúcsnál levő szögek összege:

$\displaystyle ABE\sphericalangle+EBD\sphericalangle+DBC\sphericalangle=3\cdot{60^{\circ}}=180^{\circ}$.

Ez egyenértékű azzal, hogy az ötszög $\displaystyle A, B, C$ csúcsai egy egyenesen vannak (2. ábra).

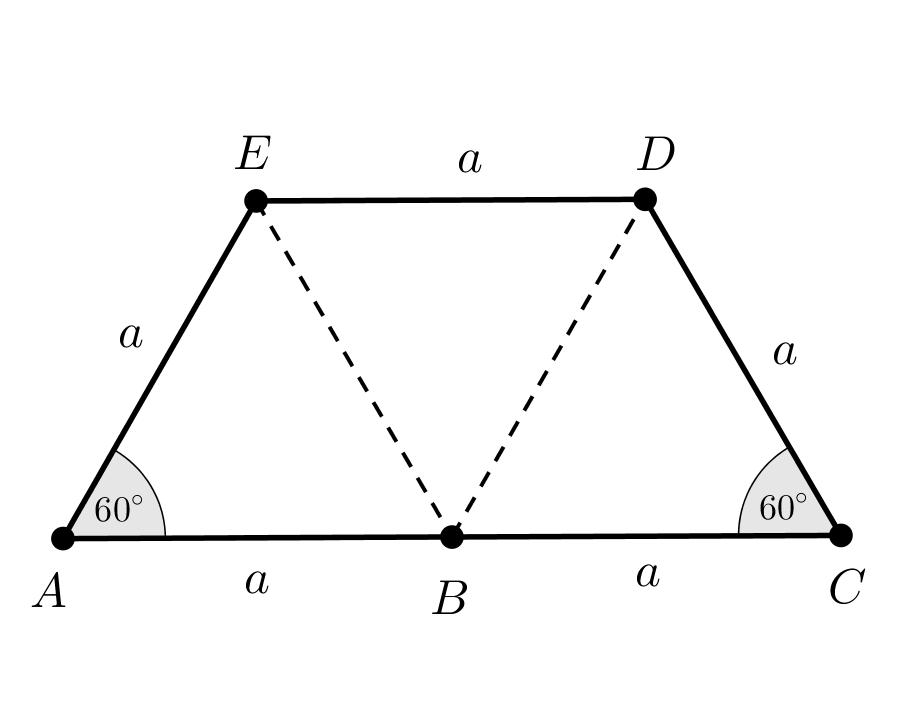
2. ábra

A 2. ábra sokszögében a feladatnak az oldalak egyenlő hosszúságára és a két $\displaystyle 60^{\circ}$-os szögre vonatkozó feltétele is teljesül, ezért az $\displaystyle EAB, BCD, BDE$ háromszögek szabályosak, így a fentiek szerint az $\displaystyle A, B, C$ pontok egy egyenesen vannak. Azonban ebben az esetben az egymáshoz csatlakozó $\displaystyle AB$ és $\displaystyle BC$ szakaszokat egyetlen $\displaystyle AC$ oldalnak kell tekintenünk, és a csatlakozási pontot, vagyis a $\displaystyle B$-t nem számítjuk a sokszög csúcsai közé, ezért nem ötszögről, hanem négyszögről van szó.

Ezzel beláttuk, hogy a feladat minden feltételét kielégítő ötszög valóban nem létezik.

Megjegyzés. Ha az ötszögről csak azt tesszük fel, hogy négy oldala egyenlő hosszú és van két $\displaystyle 60^{\circ}$-os szöge, akkor ilyen ötszög létezik.

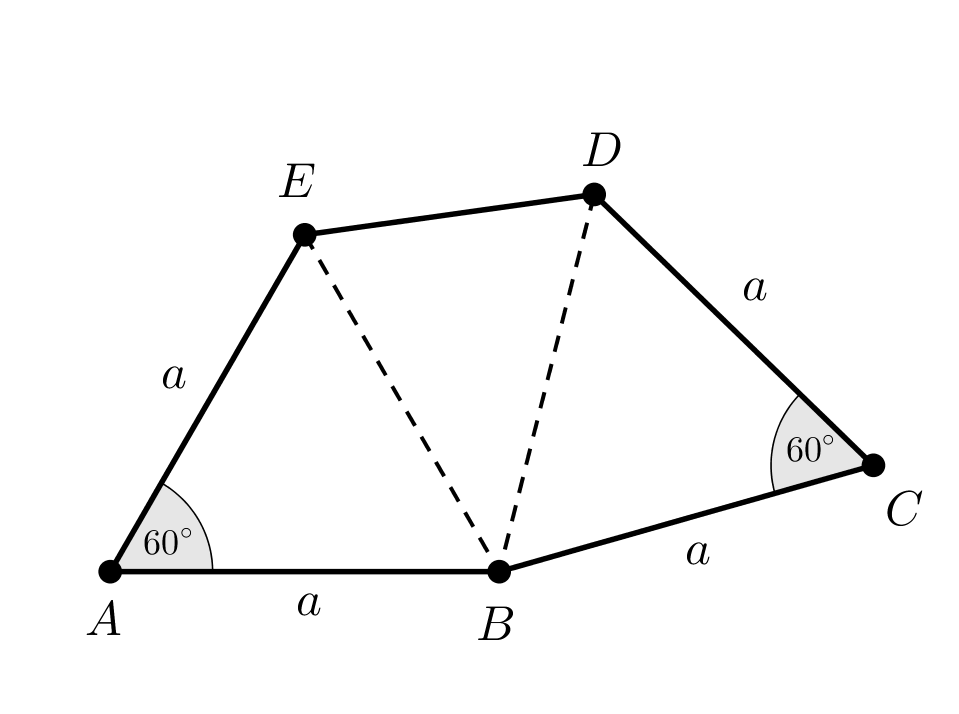
Ebben a sokszögben $\displaystyle AB=BC=CD=DA=a$ és $\displaystyle EAB\sphericalangle=BCD\sphericalangle=60^{\circ}$, ezért az $\displaystyle EAB$ és $\displaystyle BCD$ háromszögek szabályosak, de az $\displaystyle A, B, C$ csúcsok nincsenek egy egyenesen. Ekkor viszont a $\displaystyle BDE$ háromszögben csak $\displaystyle BD=BE=a$ igaz, de $\displaystyle EBD\sphericalangle<60^{\circ}$ miatt $\displaystyle DE<a$ (vagy $\displaystyle EBD\sphericalangle>60^{\circ}$ miatt $\displaystyle DE>a$), ezért a $\displaystyle BDE$ háromszög nem szabályos, azaz $\displaystyle DE\neq{a}$.

Statisztika:

237 dolgozat érkezett.
5 pontot kapott:	143 versenyző.
4 pontot kapott:	17 versenyző.
3 pontot kapott:	21 versenyző.
2 pontot kapott:	10 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	17 versenyző.
Nem versenyszerű:	3 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	3 dolgozat.

A KöMaL 2021. októberi matematika feladatai