A C. 1710. feladat (2022. március)

C. 1710. Egy egységnyi oldalú négyzetbe négy kört rajzolunk az ábrán látható módon. A két nagyobbik kör egyforma méretű és érintik egymást és a négyzet oldalait is. A két kisebbik egybevágó, ezek szintén érintik a négyzet oldalait és a nagy köröket is. Mekkora a körök középpontjai által meghatározott rombusz területe?

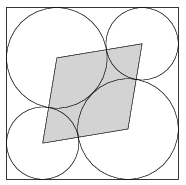
Javasolta: Gáspár Merse Előd (Budapest)

(5 pont)

A beküldési határidő 2022. április 11-én LEJÁRT.

Megoldás. Tekintsük az alábbi ábrát, amelyen a nagyobb körök sugarát $\displaystyle R$, a kisebbekét $\displaystyle r$ jelöli. A feladat feltétele miatt $\displaystyle CD=CL+LM+MD=1$.

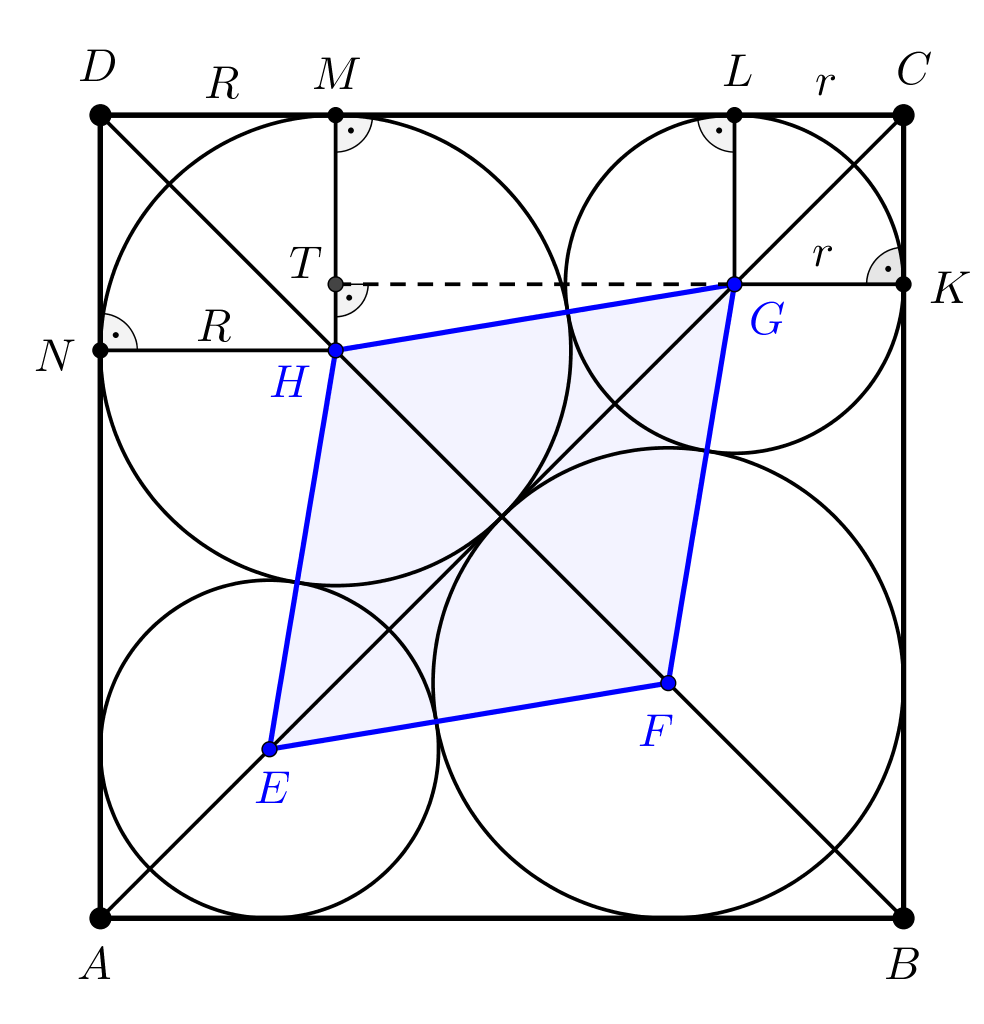
Egyszerűen belátható, hogy $\displaystyle CLGK$ és $\displaystyle DNHM$ $\displaystyle r$, illetve $\displaystyle R$ oldalú négyzetek, ezért $\displaystyle r+LM+R=1$. Kifejezzük az $\displaystyle LM$ szakasz hosszát $\displaystyle r$ és $\displaystyle R$ segítségével. Ehhez az ábrán $\displaystyle G$-ből merőlegest állítottunk $\displaystyle MH$-ra, a merőleges talppontja $\displaystyle T$. A $\displaystyle GHT$ derékszögű háromszög biztosan létrejön, hiszen $\displaystyle LG=r<R=MH$, másrészt így $\displaystyle HT=R-r$. Mivel a $\displaystyle G$ és $\displaystyle H$ középpontú körök érintik egymást, ezért $\displaystyle GH=r+R$.
Felírhatjuk a Pitagorasz-tételt a $\displaystyle GHT$ derékszögű háromszögre: $\displaystyle (r+R)^2=LM^2+(R-r)^2$, ahonnan a műveletek elvégzésével és rendezéssel $\displaystyle LM^2=4Rr$, ezért $\displaystyle LM=2\sqrt{Rr}$.

Ebből $\displaystyle r+LM+R=1$ alapján az következik, hogy

Látható, hogy az (1) egyenlőség bal oldala teljes négyzet, mégpedig $\displaystyle \big(\sqrt{r}+\sqrt{R}\big)^2=1$, innen a nyilvánvaló $\displaystyle \sqrt{r}+\sqrt{R}>0$ feltétel miatt

adódik.
Kiszámítjuk először $\displaystyle R$ értékét. Ehhez vegyük figyelembe, hogy $\displaystyle BD=\sqrt{2}, BF=DH=R\sqrt{2}$, valamint $\displaystyle FH=2R$. Eszerint $\displaystyle 2R+2R\sqrt{2}=\sqrt{2}$, ebből egyszerű átalakításokkal kapjuk, hogy $\displaystyle \displaystyle{R=\frac{1}{2+\sqrt{2}}}$, illetve a nevező négyzetgyöktelenítése után

$\displaystyle \displaystyle{R=1-\frac{\sqrt{2}}{2}}.$

Ezzel (2) alapján $\displaystyle \displaystyle{\sqrt{r}=1-\sqrt{1-\frac{\sqrt{2}}{2}}}$, innen négyzetreemeléssel és rendezéssel kapjuk, hogy

$\displaystyle \displaystyle{r=2-\frac{\sqrt{2}}{2}-\sqrt{4-2\sqrt{2}}}.$

Az $\displaystyle EFGH$ négyszög a szimmetria miatt rombusz, átlói merőlegesek egymásra, a rombusz $\displaystyle T$ területe tehát úgy is kifejezhető, hogy $\displaystyle \displaystyle{T=\frac{FH\cdot{EG}}{2}}$, és mivel $\displaystyle FH=2R$, valamint $\displaystyle EG=\sqrt{2}-2r\sqrt{2}$, ezért $\displaystyle \displaystyle{T=\frac{2R\cdot{\big(\sqrt{2}-2r\sqrt{2}\big)}}{2}}=R\cdot\big(\sqrt{2}-2r\sqrt{2}\big)$.

Az $\displaystyle R$ és $\displaystyle r$ kiszámolt értékeit behelyettesítve a műveletek elvégzése és az összevonások után

$\displaystyle T=5-4\sqrt{2}+2\cdot{\sqrt{\big(2-\sqrt{2}\big)^3}}.$

Számológéppel számolva, négy tizedesjegyre kerekítés után $\displaystyle T\approx{0.2398}$.

Statisztika:

91 dolgozat érkezett.
5 pontot kapott:	Ali Richárd, Baráth Borbála, Besze Zsolt, Cynolter Dorottya, Deák Gergely, Dukát Levente, Egyházi Hanna, Fehérvári Donát, Fekete Patrik, Fodor Dóra, Fórizs Emma, Halász Henrik, Han Ziying, Horváth Milán, Hosszu Noel, Inokai Ádám, Iván Máté Domonkos, Kerekes András, Keszthelyi Eszter, Körmöndi Márk, Kurucz Márton, Lajos Luca, Mészáros Anna Veronika, Mező Levente, Nagy 292 Korina, Nagy Daniella, Pekk Márton, Petrányi Lilla, Princz-Jakovics Anna, Radzik Réka, Richlik Márton, Sándor Eszter, Schneider Dávid, Sipeki Márton, Sütő Áron, Szabó Réka, Szabó Zóra, Szittyai Anna, Szpisják Zsófia Andrea, Tóth Gréta, Végh Lilian, Vigh 279 Zalán, Waldhauser Miklós, Werner Kinga.
4 pontot kapott:	7 versenyző.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2022. márciusi matematika feladatai