 |
A C. 1712. feladat (2022. március) |
C. 1712. Mekkorák lehetnek annak az ötszögnek az ismeretlen szögei, melynek minden oldala egyforma hosszúságú és van két derékszöge?
Javasolta: Károlyi Gergely (Budajenő)
(5 pont)
A beküldési határidő 2022. április 11-én LEJÁRT.
Megoldás. Jelöljük az \(\displaystyle ABCDE\) ötszög oldalainak hosszát \(\displaystyle a\)-val. Az ötszög két derékszöge lehet két szomszédos csúcshoz, vagy két nem szomszédos csúcshoz tartozó belső szög.
Legyen először derékszög az \(\displaystyle A\) és \(\displaystyle B\) csúcsoknál. Mivel a feladat szövege nem írta elő, hogy a négyszög konvex, ezért az \(\displaystyle ABCD\) konkáv négyszög is lehet, a két esetet az 1. ábra szemlélteti.
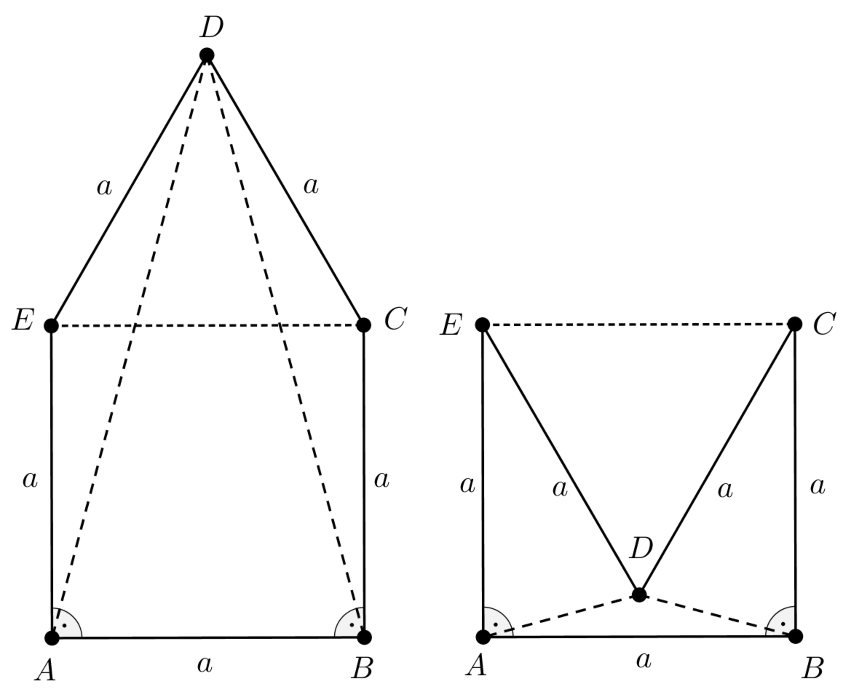
1. ábra
Mindkét esetre fennáll, hogy a két szomszédos csúcsnál levő derékszög és \(\displaystyle EA=AB=BC=a\) miatt az \(\displaystyle ABCE\) négyszög négyzet, ezért egyrészt \(\displaystyle EC=a\), másrészt \(\displaystyle BCE\sphericalangle=CEA\sphericalangle=90^{\circ}\). Az oldalak egyenlősége miatt a \(\displaystyle CDE\) háromszög mindkét esetben szabályos, így \(\displaystyle CDE\sphericalangle=DEC\sphericalangle=ECD\sphericalangle=60^{\circ}\).
Ebből azonnal következik, hogy az \(\displaystyle ABCDE\) ötszög ismeretlen szögei az 1. ábra első rajzán \(\displaystyle BCD\sphericalangle=DEA\sphericalangle=90^{\circ}+60^{\circ}=150^{\circ}\) és \(\displaystyle CDE\sphericalangle=60^{\circ}\), míg a második \(\displaystyle ABCDE\) négyszögben \(\displaystyle BCD\sphericalangle=DEA\sphericalangle=90^{\circ}-60^{\circ}=30^{\circ}\), a \(\displaystyle D\) csúcsnál pedig a \(\displaystyle CDE\sphericalangle=60^{\circ}\)-os szöget \(\displaystyle 360^{\circ}\)-ra kiegészítő, azaz \(\displaystyle 300^{\circ}\)-os belső szöget kapunk.
Ha a két derékszög két nem szomszédos csúcsnál helyezkedik el, akkor nem sérti az általánosságot, ha feltesszük, hogy a két derékszögű csúcs a \(\displaystyle C\) és az \(\displaystyle E\).
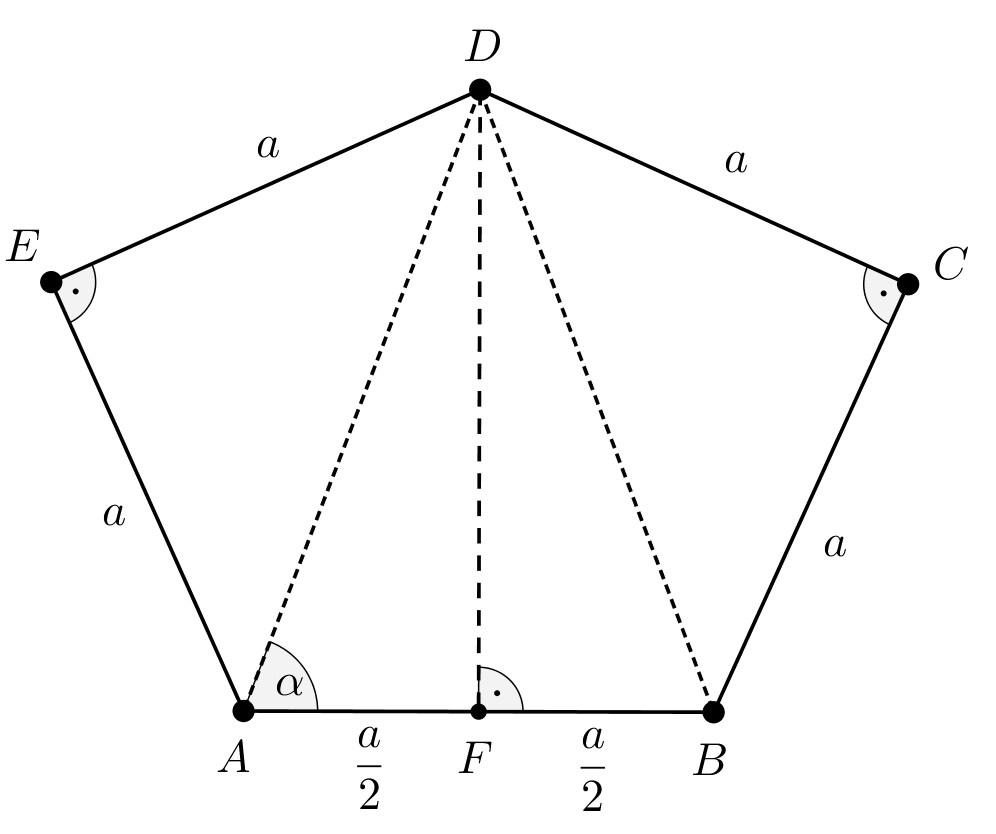
2. ábra
Konkáv négyszöget ezúttal is létrehozhatnánk, például úgy, hogy az \(\displaystyle ABC\) háromszöget a \(\displaystyle AC\)-re, vagy a \(\displaystyle BCD\) háromszöget a \(\displaystyle BD\)-re, vagy a \(\displaystyle CDE\) háromszöget a \(\displaystyle CE\)-re tükrözzük, az így kapott konkáv ötszögek mindegyikére teljesülni fog, hogy az oldalaik egyenlő hosszúak, de minden ilyen eset ellenkezne azzal a feltétellel, hogy az ötszögben a két szemben levő szög derékszög, mert a tükrözés legalább az egyik \(\displaystyle 90^{\circ}\)-os belső szöget megváltoztatná. Ezért ezúttal nem kapunk konkáv ötszöget.
A 2. ábrán a \(\displaystyle DE=AE=DC=BC=a\) feltétel és a derékszögek miatt \(\displaystyle ADE\) és \(\displaystyle BCD\) egyenlő szárú derékszögű háromszögek, ebből \(\displaystyle AD=BD=a\sqrt{2}\), illetve \(\displaystyle DAE\sphericalangle=ADE\sphericalangle=DBC\sphericalangle=BDC\sphericalangle=45^{\circ}\).
Az \(\displaystyle ABD\) egyenlő szárú háromszög \(\displaystyle AB\) oldalának felezőpontját \(\displaystyle F\)-fel jelöltük, a háromszög alapon fekvő szögei \(\displaystyle BAD\sphericalangle=ABD\sphericalangle=\alpha\).
Az \(\displaystyle AFD\) derékszögű háromszögben felírhatjuk, hogy \(\displaystyle \displaystyle{\cos{\alpha}=\frac{AF}{AD}=\frac{\frac{a}{2}}{a\sqrt{2}}=\frac{1}{2\sqrt{2}}}\). Ebből számológép segítségével azt kapjuk, hogy \(\displaystyle \alpha{\approx69,295^{\circ}}\) és emiatt \(\displaystyle ADF\sphericalangle\approx{20,705^{\circ}}\).
Az \(\displaystyle ABCDE\) ötszög ismeretlen szögei ebben az esetben \(\displaystyle EAB\sphericalangle=CBA\sphericalangle=\alpha+45^{\circ}\approx{114,295^{\circ}}\) és \(\displaystyle EDC\sphericalangle=2\cdot45^{\circ}+2\cdot{ADF\sphericalangle}\approx{131,41^{\circ}}\). Ezzel a feladatot megoldottuk.
Statisztika:
39 dolgozat érkezett. 5 pontot kapott: Besze Zsolt, Cynolter Dorottya, Pekk Márton, Rumpler Bianka, Sipeki Márton, Szabó Zóra, Szegedi Ágoston, Tóth Gréta, Waldhauser Miklós. 4 pontot kapott: Egyházi Hanna, Radzik Réka, Schneider Dávid, Szalanics Tamás, Werner Kinga. 3 pontot kapott: 15 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 2 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2022. márciusi matematika feladatai
