 |
A C. 1718. feladat (2022. április) |
C. 1718. Egy síkon elhelyeztünk 8 darab egységnyi élű kockát, majd ezekre még 5 darab egységkockát tettünk az ábra szerint.
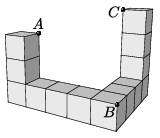
Határozzuk meg az \(\displaystyle ABC\) háromszög oldalainak hosszát.
(5 pont)
A beküldési határidő 2022. május 10-én LEJÁRT.
Megoldás. Az alábbi ábrán az \(\displaystyle A,B,C\) pontokon kívül megjelöltük még a \(\displaystyle D,E,F,G,H,K\) pontokat. Az \(\displaystyle EDB\) és \(\displaystyle GFB\) háromszögek a kockák egy csúcsban találkozó éleinek merőlegessége miatt derékszögű háromszögek, éspedig a \(\displaystyle D\), illetve \(\displaystyle F\) pontokban.
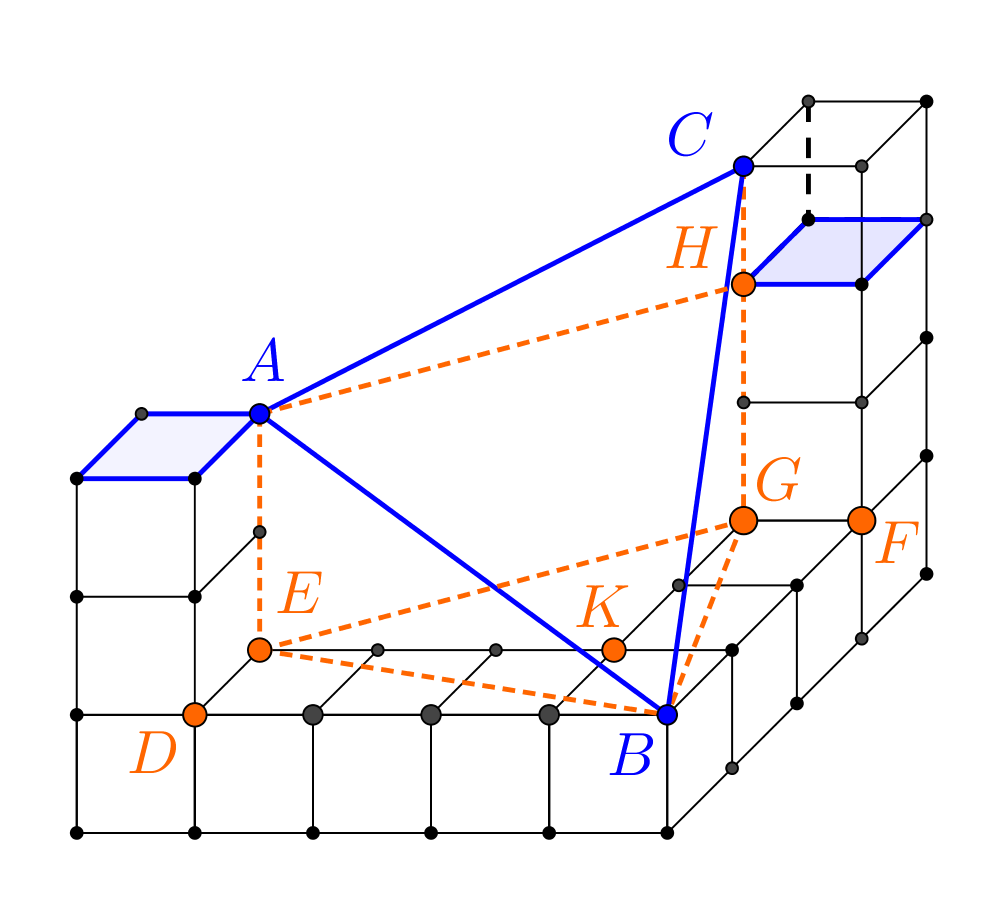
A Pitagorasz-tételből ezért
| \(\displaystyle (1)\) | \(\displaystyle BE^2=1^2+4^2=17, \quad BG^2=1^2+3^2=10.\) |
Az \(\displaystyle AE=2\) szakasz merőleges az alapsíkkal párhuzamos kockalapokra, és így a \(\displaystyle BE\) szakaszra is. Hasonlóan indokolhatjuk, hogy a \(\displaystyle CG\) szakasz merőleges \(\displaystyle BG\)-re.
Eszerint az \(\displaystyle AEB\) és \(\displaystyle CGB\) az \(\displaystyle E\), illetve \(\displaystyle G\) pontban derékszögű háromszögek. Ezért a Pitagorasz-tétel és az (1) összefüggések felhasználásával \(\displaystyle AB^2=AE^2+BE^2=21\), azaz \(\displaystyle AB=\sqrt{21}\), valamint \(\displaystyle BC^2=CG^2+BG^2=19\), azaz \(\displaystyle BC=\sqrt{19}\).
Az előzőekhez hasonlóan egyszerűen látható, hogy \(\displaystyle EKG\) a \(\displaystyle K\) csúcsban derékszögű háromszög, ezért \(\displaystyle EG^2=3^2+2^2=13\), vagyis \(\displaystyle EG=\sqrt{13}\). Ugyanakkor világos, hogy \(\displaystyle AE\) és \(\displaystyle HG\) párhuzamos és egyenlő hosszúságú szakaszok, ami azt jelenti, hogy \(\displaystyle AEGH\) paralelogramma. Eszerint \(\displaystyle AH=EG=\sqrt{13}\).
Az \(\displaystyle A, H\) pontok a kockák elhelyezkedése miatt az alapsíktól egyaránt 3 egység távolságra vannak, vagyis \(\displaystyle AH\) párhuzamos az alapsíkkal, de akkor \(\displaystyle AH\) merőleges az alapsíkkal derékszöget bezáró \(\displaystyle CH\) szakaszra, tehát \(\displaystyle AHC\) is derékszögű háromszög. Ismét a Pitagorasz-tétellel számolva \(\displaystyle CA^2=AH^2+CH^2=14\), tehát \(\displaystyle CA=\sqrt{14}\).
Az \(\displaystyle ABC\) háromszög oldalainak hossza tehát \(\displaystyle AB=\sqrt{21},\quad BC=\sqrt{19}, \quad CA=\sqrt{14}\).
Statisztika:
187 dolgozat érkezett. 5 pontot kapott: 80 versenyző. 4 pontot kapott: 37 versenyző. 3 pontot kapott: 19 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 11 versenyző. Nem versenyszerű: 16 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2022. áprilisi matematika feladatai
