 Problem C. 1727. (May 2022)
Problem C. 1727. (May 2022)
C. 1727. In a solid sphere of radius \(\displaystyle R\), a cylindrical bore of radius \(\displaystyle r<R\) is made along a line passing through its centre. Express the volume of the remaining solid in terms of the height \(\displaystyle m\) of the remaining solid.
Proposed by B. Szabó, Miskolc, 1986
(5 pont)
Deadline expired on June 10, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Messük el a gömböt a gömb \(\displaystyle O\) középpontján átmenő olyan síkkal, amely a henger \(\displaystyle t\)-vel jelölt tengelyét tartalmazza. Ez a sík a gömbből kimetszi a \(\displaystyle 2R\) átmérőjű kört, a hengerből pedig az \(\displaystyle ABCD\) téglalapot. Az \(\displaystyle ABCD\) téglalap oldalaira \(\displaystyle AB=CD=2r\) és \(\displaystyle BC=DA=m\) teljesül. Tekintsük az alábbi ábrát.
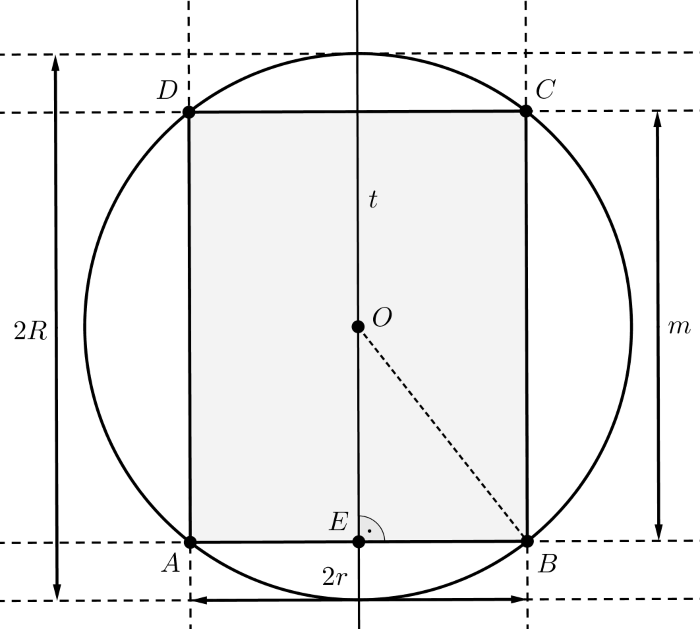
A gömbnek a feladatban leírt átfúrása után a gömbből hiányozni fog egyrészt az a két gömbsüveg, amelyek alaplapja az \(\displaystyle AB\), illetve \(\displaystyle CD\) átmérőjű kör, magassága pedig \(\displaystyle \displaystyle{h=R-\frac{m}{2}}\), másrészt pedig a henger, amelynek alapköre \(\displaystyle r\) sugarú, magassága \(\displaystyle m\). A gömb térfogata \(\displaystyle \displaystyle{V_g=\frac{4R^3\cdot{\pi}}{3}}\), a henger térfogata \(\displaystyle \displaystyle{V_h=r^2\cdot{\pi}\cdot{m}}\), az \(\displaystyle R\) sugarú gömbből levágott és \(\displaystyle r\) sugarú alapkörrel rendelkező, \(\displaystyle h\) magasságú gömbsüveg térfogata \(\displaystyle \displaystyle{V_s=\frac{\pi\cdot{h^2}\cdot{\big(3R-h\big)}}{3}}\).
A gömb átfúrása után keletkező maradéktest térfogata
\(\displaystyle \displaystyle{V_m=V_g-2V_s-V_h},\)
azaz
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{V_m=\frac{4R^3\cdot{\pi}}{3}-\frac{2\pi\cdot{h^2}\cdot{\big(3R-h\big)}}{3}}-r^2\cdot{\pi}\cdot{m}.\) |
Az (1) egyenlet jobb oldalán kiemeljük a \(\displaystyle \displaystyle{\frac{\pi}{3}}\) tényezőt és beírjuk a \(\displaystyle \displaystyle{h=R-\frac{m}{2}}\) összefüggést:
\(\displaystyle \displaystyle{V_m=\frac{\pi}{3}\cdot{\Bigg[4R^3-2\Big(R-\frac{m}{2}\Big)^2\cdot{\Big(2R+\frac{m}{2}\Big)}-3r^2\cdot{m}\Bigg]}}.\)
A műveletek elvégzése és rendezés után azt kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{V_m=\frac{\pi}{3}\cdot{\Bigg[3R^2m-\frac{m^3}{4}-3r^2m}\Bigg]}.\) |
Írjuk fel most az ábra \(\displaystyle OEB\) derékszögű háromszögére a Pitagorasz-tételt, eszerint \(\displaystyle \displaystyle{r^2+\frac{m^2}{4}=R^2}\), ezt a (2) egyenletbe helyettesítve a műveletek elvégzése és egyszerűsítés után adódik, hogy
\(\displaystyle \displaystyle{V_m=\frac{\pi\cdot{m^3}}{6}},\)
ezzel megadtuk a maradéktest térfogatát az \(\displaystyle m\) magasságának függvényében.
Statistics:
22 students sent a solution. 5 points: Cynolter Dorottya, Horváth Milán, Keszthelyi Eszter, Kurucz Márton, Nagy Daniella, Pekk Márton, Szabó Réka, Szalanics Tamás, Waldhauser Miklós, Werner Kinga. 2 points: 1 student. 1 point: 7 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, May 2022
