 |
A C. 1728. feladat (2022. szeptember) |
C. 1728. Határozzuk meg a
\(\displaystyle -\frac{1}{6}x+\frac{1}{2}=\{x\} \)
egyenlet megoldásainak pontos értékét.
(\(\displaystyle \{x\}\) az \(\displaystyle x\) törtrésze, vagyis az \(\displaystyle x\)-nek és \(\displaystyle x\)-nél nem nagyobb egészek legnagyobbikának különbsége.)
(5 pont)
A beküldési határidő 2022. október 10-én LEJÁRT.
Megoldás. Közös koordináta-rendszerben ábrázoljuk az \(\displaystyle f(x)=-\frac{1}{6}x+\frac{1}{2}\) és a \(\displaystyle g(x)=\{x\}\) függvényt (lásd ábra).
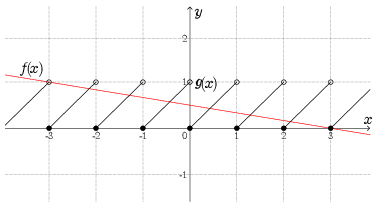
A két függvény grafikonjának \(\displaystyle 7\) közös pontja van, ezért az egyenletnek \(\displaystyle 7\) megoldása van, amelyek pontos értékét az alábbiak szerint határozzuk meg. A törtrész függvény szigorúan monoton növekvő darabkái éppen az \(\displaystyle m=1\) meredekségű, az \(\displaystyle y\)-tengelyt \(\displaystyle b\in \mathbb{Z}\)-ben metsző lineáris függvények megfelelő leszűkítései. Esetünkben a metszéspontok ott találhatóak, ahol \(\displaystyle 0 \leq f(x) < 1\). Ez \(\displaystyle -3 \leq b \leq 3\)-ra teljesül, így a következő paraméteres egyenletet kell megoldanunk:
\(\displaystyle -\frac{1}{6}x+\frac{1}{2}=x+b,\)
ebből rendezés után az
\(\displaystyle x=\frac{3-6b}{7}\)
megoldást kapjuk, amelybe behelyettesítjük a megfelelő \(\displaystyle b\) értékeket.
Ha \(\displaystyle b=3\), akkor \(\displaystyle \displaystyle{x_1=\frac{3-18}{7}=-\frac{15}{7}}\).
Ha \(\displaystyle b=2\), akkor \(\displaystyle \displaystyle{x_2=-\frac{9}{7}}\).
Ha \(\displaystyle b=1\), akkor \(\displaystyle \displaystyle{x_3=-\frac{3}{7}}\).
Ha \(\displaystyle b=0\), akkor \(\displaystyle \displaystyle{x_4=\frac{3}{7}}\).
Ha \(\displaystyle b=-1\), akkor \(\displaystyle \displaystyle{x_5=\frac{9}{7}}\).
Ha \(\displaystyle b=-2\), akkor \(\displaystyle \displaystyle{x_6=\frac{15}{7}}\).
Ha \(\displaystyle b=-3\), akkor \(\displaystyle \displaystyle{x_7=\frac{21}{7}=3}\).
A megoldások helyességéről behelyettesítéssel győződhetünk meg.
Megjegyzés. A feladatnak a függvények ábrázolása után geometriai, illetve koordináta-geometriai értelmezést is adhatunk. Tekintsük az alábbi ábrán látható \(\displaystyle ABC\) háromszöget. Az egyenlet megoldásai azon pontok első koordinátái, amelyek az \(\displaystyle f(x)\) és \(\displaystyle g(x)\) függvények grafikonjainak metszéspontjai. Ezek az ábrán a \(\displaystyle P,Q,R,S,T,U,B\) pontok. A \(\displaystyle C\) pont nem tartozik hozzá a \(\displaystyle g(x)\) függvény grafikonjához, így \(\displaystyle x=-3\) nyilván nem megoldás.
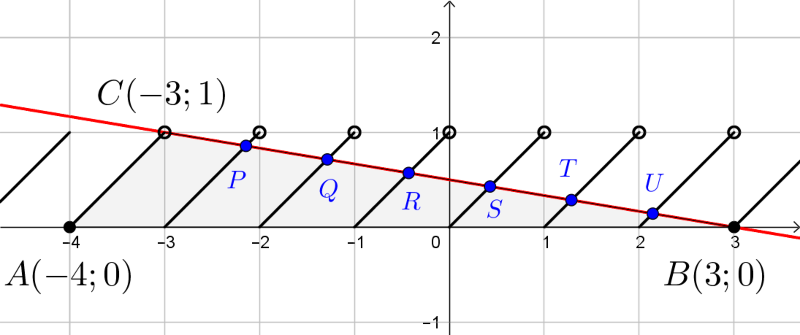
A háromszög \(\displaystyle AB\) oldalát a szakaszra eső belső rácspontok \(\displaystyle 7\) egyenlő részre osztják, továbbá a \(\displaystyle g(x)=\{x\}\) függvény grafikonjának egyes darabjai egymással párhuzamos egyenesekre illeszkednek, ezért a párhuzamos szelők tételéből az következik, hogy a \(\displaystyle P,Q,R,S,T,U\) pontok a \(\displaystyle BC\) szakasz hetedelőpontjai. Ez azt is jelenti, hogy a \(\displaystyle B,C\) pontok koordinátáinak ismeretében a \(\displaystyle P,Q,R,S,T,U\) pontok első koordinátái meghatározhatók.
Ezek a következők:
\(\displaystyle \displaystyle{x_P=\frac{6\cdot{(-3)}+3}{7}=-\frac{15}{7}},\)
\(\displaystyle \displaystyle{x_Q=\frac{5\cdot{(-3)}+2\cdot{3}}{7}=-\frac{9}{7}},\)
\(\displaystyle \displaystyle{x_R=\frac{4\cdot{(-3)}+3\cdot{3}}{7}=-\frac{3}{7}},\)
\(\displaystyle \displaystyle{x_S=\frac{3\cdot{(-3)}+4\cdot{3}}{7}=\frac{3}{7}},\)
\(\displaystyle \displaystyle{x_T=\frac{2\cdot{(-3)}+5\cdot{3}}{7}=\frac{9}{7}},\)
\(\displaystyle \displaystyle{x_U=\frac{1\cdot{(-3)}+6\cdot{3}}{7}=\frac{15}{7}},\)
ezek éppen a feladat megoldásában kapott értékek.
Nyilvánvaló, hogy a \(\displaystyle B\) pont első koordinátája, azaz \(\displaystyle x=3\) is megfelel az egyenletnek, így összesen valóban 7 megoldása van a feladatnak.
Statisztika:
236 dolgozat érkezett. 5 pontot kapott: 108 versenyző. 4 pontot kapott: 16 versenyző. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 13 versenyző. 1 pontot kapott: 10 versenyző. 0 pontot kapott: 33 versenyző. Nem versenyszerű: 24 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2022. szeptemberi matematika feladatai
