 Problem C. 1741. (November 2022)
Problem C. 1741. (November 2022)
C. 1741. The diagonals \(\displaystyle AC\) and \(\displaystyle BD\) of a convex quadrilateral \(\displaystyle ABCD\) intersect at \(\displaystyle M\). Is it possible that the areas of triangles \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\) and \(\displaystyle DAM\), in this order, are four consecutive terms of
\(\displaystyle a)\) an arithmetic sequence;
\(\displaystyle b)\) a geometric sequence?
Proposed by B. Bíró, Eger
(5 pont)
Deadline expired on December 12, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük az \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\), \(\displaystyle DAM\) háromszög területét rendre \(\displaystyle T_1\), \(\displaystyle T_2\), \(\displaystyle T_3\), \(\displaystyle T_4\)-gyel. Először bizonyítani fogjuk, hogy az \(\displaystyle ABM\) és \(\displaystyle CDM\) háromszögek területének szorzata megegyezik a \(\displaystyle BCM\) és \(\displaystyle DAM\) háromszögek területének szorzatával, azaz \(\displaystyle \displaystyle{T_1\cdot{T_3}=T_2\cdot{T_4}}\).
A feltételeknek megfelelő ábrán megrajzoltuk az \(\displaystyle ABC\) és \(\displaystyle CDA\) háromszögek \(\displaystyle B\), illetve \(\displaystyle D\) csúcsához tartozó \(\displaystyle BE\) és \(\displaystyle DF\) magasságát.
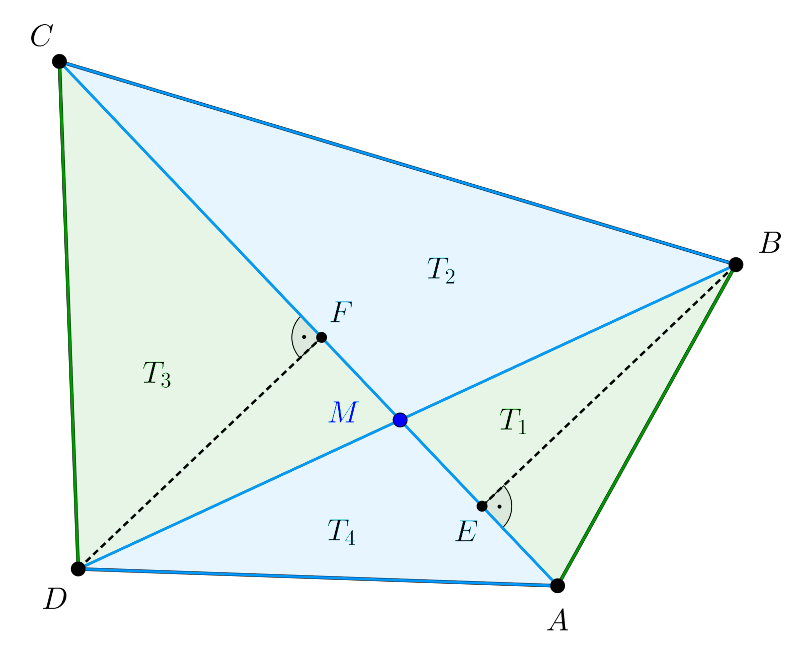
Az \(\displaystyle ABM\), illetve \(\displaystyle BCM\) háromszögek \(\displaystyle T_1\), illetve \(\displaystyle T_2\) területére \(\displaystyle \displaystyle{T_1=\frac{AM\cdot{BE}}{2}}\), illetve \(\displaystyle \displaystyle{T_2=\frac{CM\cdot{BE}}{2}}\), ezért a két terület aránya
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\frac{T_1}{T_2}=\frac{AM}{CM}}.\) |
Hasonlóan egyszerű módon láthatjuk be a \(\displaystyle DAM\) és \(\displaystyle CDM\) háromszögeknek az \(\displaystyle AM\), illetve \(\displaystyle CM\) oldalak közös \(\displaystyle DF\) magasságának segítségével, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\frac{T_4}{T_3}=\frac{AM}{CM}}.\) |
Az (1) és (2) egyenletek jobb oldalainak egyenlőségéből a bal oldalak egyenlősége nyilvánvalóan következik, ebből pedig
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{T_1\cdot{T_3}=T_2\cdot{T_4}}.\) |
Tegyük fel, hogy a \(\displaystyle T_1, T_2, T_3, T_4\) területek ebben a sorrendben egy nemkonstans számtani sorozat közvetlen egymás utáni tagjai. Ez akkor és csak akkor lehetséges, ha a számtani sorozat különbségét \(\displaystyle d\)-vel jelölve egyrészt \(\displaystyle d\neq{0}\), másrészt
\(\displaystyle \displaystyle{T_2=T_1+d,\quad{T_3=T_1+2d,}\quad {T_4=T_1+3d}}.\)
Ebből a (3) összefüggés alapján azt kapjuk, hogy
\(\displaystyle \displaystyle{T_1\cdot\big({T_1+2d}\big)=\big(T_1+d\big)\cdot\big({T_1+3d}\big)},\)
amelyből a műveletek elvégzésével és rendezéssel
\(\displaystyle 2T_1\cdot{d}+3d^2=0\)
adódik. A kapott egyenlet bal oldalát szorzattá alakítjuk:
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{d\cdot\big(2T_1+3d\big)=0}.\) |
A (4) egyenlet szerint \(\displaystyle d=0\) vagy \(\displaystyle 2T_1+3d=0\) lehetséges.
Mivel \(\displaystyle d\neq{0}\), ez azt jelenti, hogy a négy háromszög területe nem egyenlő.
Ezért csak \(\displaystyle 2T_1+3d=0\) állhat fenn, azaz ekkor \(\displaystyle \displaystyle{T_1=-\frac{3}{2}d}\), ez pedig csak úgy lehetséges, ha \(\displaystyle d<0\), vagyis a \(\displaystyle T_1, T_2, T_3, T_4\) számok egy csökkenő számtani sorozat egymás utáni tagjai. Ez azonban nem valósulhat meg, mert ebből \(\displaystyle \displaystyle{d=-\frac{2}{3}T_1}\) következne, innen pedig \(\displaystyle \displaystyle{T_3=-\frac{1}{3}T_1}\), illetve \(\displaystyle T_4=-T_1\) adódna. Ez pedig nyilván nem lehetséges, mert a háromszögek területei pozitív számok.
A feladat \(\displaystyle a)\) kérdésére tehát az a válasz, hogy az \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\), \(\displaystyle DAM\) háromszögek területei ebben a sorrendben nem lehetnek egy nemkonstans számtani sorozat közvetlen egymás utáni tagjai.
Tegyük fel most, hogy a \(\displaystyle T_1, T_2, T_3, T_4\) területek számértéke ebben a sorrendben egy nemkonstans mértani sorozat közvetlen egymás utáni tagjai.
Ez akkor és csakis akkor lehetséges, ha a területek nem egyenlők és a \(\displaystyle T_2\) terület a \(\displaystyle T_1\) és \(\displaystyle T_3\) mértani közepe, a \(\displaystyle T_3\) terület pedig a \(\displaystyle T_2\) és \(\displaystyle T_4\) mértani közepe, vagyis
\(\displaystyle \displaystyle{T_2=\sqrt{T_1\cdot{T_3}},\quad T_3=\sqrt{T_2\cdot{T_4}}},\)
ebből azonban (3) szerint az következik, hogy
| \(\displaystyle (5)\) | \(\displaystyle T_2=T_3.\) |
A \(\displaystyle T_2\) és \(\displaystyle T_3\) számok egy mértani sorozat közvetlen egymás utáni tagjai, ezért (5) pontosan akkor valósulhat meg, ha a mértani sorozat \(\displaystyle q\) hányadosára \(\displaystyle q=1\) teljesül, azaz a mértani sorozat tagjai mind egyenlők.
Ez azonban a feltétel miatt nem lehetséges, így az \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\), \(\displaystyle DAM\) háromszögek területei ebben a sorrendben egy nemkonstans mértani sorozat tagjai sem lehetnek.
A feladat mindkét részében nemleges választ kaptunk.
Megjegyzés. Ha megengednénk, hogy a feladatban szereplő sorozatok konstansok is lehetnek, akkor arra az eredményre jutnánk, hogy a \(\displaystyle T_1, T_2, T_3, T_4\) területek számértéke mind számtani, mind mértani sorozat esetén egyenlő. Könnyen belátható, hogy ekkor az \(\displaystyle ABCD\) négyszög csak paralelogramma lehet.
Statistics:
32 students sent a solution. 5 points: Baksa Anna, Bilicki Vilmos, Braun Zsófia, Fekete Patrik, Hajós Balázs, Halász Henrik, Kéki Edit, Keszthelyi Eszter, Laskai Botond, Mészáros Anna Veronika, Schneider Dávid, Sipeki Márton, Végh Lilian, Waldhauser Miklós. 4 points: Fiser 234 Boldizsár, Seprődi Barnabás Bendegúz, Tomesz László Gergő. 3 points: 4 students. 2 points: 2 students. 1 point: 2 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, November 2022
