 |
A C. 1744. feladat (2022. december) |
C. 1744. Az \(\displaystyle ABC\) háromszögben \(\displaystyle CAB\sphericalangle=45^{\circ}\) és \(\displaystyle ABC\sphericalangle=60^{\circ}\). Az \(\displaystyle AB\) szakasz egy pontja \(\displaystyle D\). A \(\displaystyle CAD\) háromszög körülírt köre áthalad az \(\displaystyle ABC\) háromszög magasságpontján. Határozzuk meg az \(\displaystyle \frac{AD}{BD}\) arány pontos értékét úgy, hogy a megoldás során nem használunk szögfüggvényeket.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2023. január 10-én LEJÁRT.
Megoldás. Jelöljük a háromszög oldalait a szokásos módon, azaz \(\displaystyle BC=a, CA=b, AB=c\).
Az \(\displaystyle ABC\) háromszög harmadik szöge nyilván \(\displaystyle BCA\sphericalangle=75^{\circ}\), tehát a háromszög minden szöge hegyesszög. Ebből az is következik, hogy a háromszög \(\displaystyle M\) magasságpontja a háromszög belső pontja. Tekintsük a következő ábrát, amelyen az \(\displaystyle A\) és \(\displaystyle C\) pontból húzott magasságok talppontja \(\displaystyle E\), illetve \(\displaystyle F\).
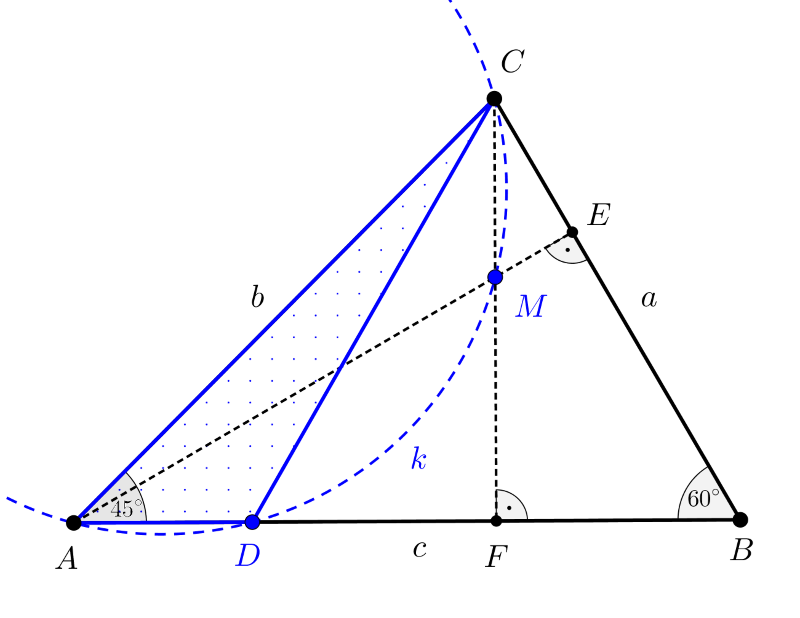
A keresett \(\displaystyle D\) pont csak az \(\displaystyle AF\) szakasz belső pontja lehet, ellenkező esetben az \(\displaystyle CAD\) háromszög \(\displaystyle k\) körülírt körének az \(\displaystyle M\) egy belső pontja lenne, így \(\displaystyle k\) nem haladhatna át az \(\displaystyle M\) magasságponton.
A \(\displaystyle BEMF\) négyszög húrnégyszög, mert az \(\displaystyle E\) és \(\displaystyle F\) csúcsoknál levő belsző szögek derékszögek, így összegük \(\displaystyle 180^{\circ}\). Ekkor
\(\displaystyle EMF\sphericalangle=180^{\circ}-EBF\sphericalangle=120^{\circ}.\)
Mivel \(\displaystyle EMF\sphericalangle\) és \(\displaystyle CMA\sphericalangle\) csúcsszögek, ezért \(\displaystyle CMA\sphericalangle=120^{\circ}\) is teljesül.
A \(\displaystyle k\) körre illeszkednek a \(\displaystyle C\), \(\displaystyle M\), \(\displaystyle D\), \(\displaystyle A\) pontok és a kerületi szögek tétele alapján a \(\displaystyle D\) pontból a \(\displaystyle CA=b\) húr ugyanakkora szögben látszik, mint az \(\displaystyle M\) pontból, ezért \(\displaystyle CDA\sphericalangle=120^{\circ}\), vagyis
| \(\displaystyle (1)\) | \(\displaystyle CDB\sphericalangle=60^{\circ}.\) |
Az (1) eredmény szerint a \(\displaystyle CDB\) háromszög minden szöge \(\displaystyle 60^{\circ}\)-os, tehát ez a háromszög szabályos, és emiatt \(\displaystyle BC=CD=DB=a\), vagyis \(\displaystyle AD=c-a\). Ebből következik, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\frac{AD}{BD}=\frac{c-a}{a}}.\) |
A \(\displaystyle CDB\) szabályos háromszög \(\displaystyle CF\) magasságának hossza \(\displaystyle \displaystyle{CF=\frac{a\sqrt{3}}{2}}\). Mivel a \(\displaystyle CAF\) háromszög nyilvánvalóan egyenlő szárú derékszögű háromszög, ezért \(\displaystyle \displaystyle{AF=\frac{a\sqrt{3}}{2}}\) is fennáll.
Ugyanakkor \(\displaystyle AD+DF=AF\), azaz \(\displaystyle \displaystyle{c-a+\frac{a}{2}=\frac{a\sqrt{3}}{2}}\), ahonnan rendezés után azt kapjuk, hogy
\(\displaystyle \displaystyle{c-a=\frac{a\cdot\big(\sqrt{3}-1\big)}{2}},\)
ebből pedig \(\displaystyle a\)-val való osztás után
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{\frac{c-a}{a}=\frac{\sqrt{3}-1}{2}}.\) |
A (2) és (3) eredmény összevetésével kapjuk a feladat megoldását: a feltételek mellett az \(\displaystyle AD\) és \(\displaystyle BD\) szakaszok arányának pontos értéke
\(\displaystyle \displaystyle{\frac{AD}{BD}=\frac{\sqrt{3}-1}{2}}.\)
Statisztika:
102 dolgozat érkezett. 5 pontot kapott: 60 versenyző. 4 pontot kapott: 11 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 2 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2022. decemberi matematika feladatai
