 Problem C. 1746. (December 2022)
Problem C. 1746. (December 2022)
C. 1746. Side \(\displaystyle AB\) of a square \(\displaystyle ABCD\) is extended beyond point \(\displaystyle A\) by the line segment \(\displaystyle AE=2\), and beyond point \(\displaystyle B\) by the line segment \(\displaystyle BF=3\). Lines \(\displaystyle ED\) and \(\displaystyle FC\) enclose an angle of \(\displaystyle 45^{\circ}\). Determine the possible values of the length of the sides of the square.
Proposed by L. Németh, Fonyód
(5 pont)
Deadline expired on January 10, 2023.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Legyen az \(\displaystyle ABCD\) négyzet oldalának hossza \(\displaystyle x\), az \(\displaystyle ED\) és \(\displaystyle FC\) egyenesek metszéspontja \(\displaystyle M\). Ha az egyenesek \(\displaystyle 45^{\circ}\)-os szöget zárnak be, akkor két eset lehetséges: \(\displaystyle EMF\sphericalangle=45^{\circ}\), vagy \(\displaystyle EMF\sphericalangle=135^{\circ}\). Húzzunk párhuzamost a \(\displaystyle D\) ponton keresztül az \(\displaystyle MF\) egyenessel, ez az \(\displaystyle AB\) egyenesét az \(\displaystyle N\) pontban metszi.
Tekintsük az alábbi vázlatos ábrát, amelyen \(\displaystyle EMF\sphericalangle=\delta\) és \(\displaystyle MFE\sphericalangle=\varphi\).
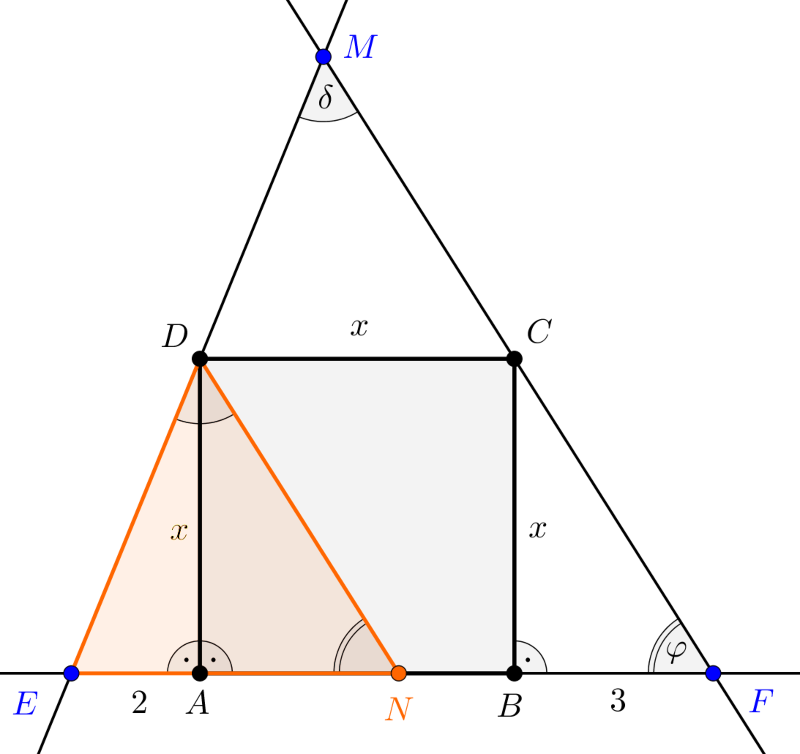
Mivel \(\displaystyle CD\parallel{AB}\) és \(\displaystyle CF\parallel{DN}\), ezért egyrészt \(\displaystyle CDNF\) paralelogramma, és így \(\displaystyle CF=DN\), másrészt \(\displaystyle DNA\sphericalangle\) és \(\displaystyle CFB\sphericalangle\) egyállású szögek, tehát egyenlők, azaz \(\displaystyle DNA\sphericalangle=\varphi\).
A \(\displaystyle DNA\) és \(\displaystyle CFB\) háromszögek szögei egyenlő nagyságúak és mivel a két háromszögben \(\displaystyle CF=DN\), ezért a két háromszög egybevágó, emiatt \(\displaystyle AN=3\).
A \(\displaystyle DNA\) és \(\displaystyle DEA\) derékszögű háromszögekre felírt Pitagorasz-tételekből következik, hogy
\(\displaystyle \displaystyle{DN=\sqrt{x^2+9}; \quad DE=\sqrt{x^2+4}}.\)
A \(\displaystyle DNA\) háromszögben \(\displaystyle DNA\sphericalangle=\varphi\), ezért
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\sin{\varphi}=\frac{DA}{DN}=\frac{x}{\sqrt{x^2+9}}}.\) |
Ugyanakkor a \(\displaystyle DN\) és \(\displaystyle MF\) párhuzamosságából az is következik, hogy \(\displaystyle EDN\sphericalangle=\delta\), és ezért \(\displaystyle \sin{EDN\sphericalangle}=\sin{\delta}\).
A feltételek miatt \(\displaystyle \delta=45^{\circ}\) vagy \(\displaystyle \delta=135^{\circ}\), ezért
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\sin{\delta}=\sin{45^{\circ}}=\sin{135^{\circ}}=\frac{\sqrt{2}}{2}}.\) |
Felírjuk a szinusztételt a \(\displaystyle DNE\) háromszögben:
\(\displaystyle \displaystyle{\frac{DE}{NE}=\frac{\sin{\varphi}}{\sin{\delta}}},\)
ebből \(\displaystyle DE=\sqrt{x^2+4}\) és \(\displaystyle NE=5\), illetve (1), valamint (2) alapján
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{\frac{\sqrt{x^2+4}}{5}=\frac{\frac{x}{\sqrt{x^2+9}}}{\frac{\sqrt{2}}{2}}}\) |
következik.
A (3) egyenletből négyzetreemelés és a műveletek elvégzése után \(\displaystyle \big(x^2+4\big)\cdot\big(x^2+9\big)=50x^2\), innen pedig
| \(\displaystyle (4)\) | \(\displaystyle x^4-37x^2+36=0\) |
adódik.
A (4) egyenletből \(\displaystyle x^2\) értékére két megoldást kapunk: \(\displaystyle x^2=1\) és \(\displaystyle x^2=36\).
Az \(\displaystyle x\) csak pozitív szám lehet, ezért az \(\displaystyle ABCD\) négyzet oldalhosszának értéke \(\displaystyle x=1\) és \(\displaystyle x=6\) lehet.
Trigonometriai úton, például a \(\displaystyle DNE\) háromszög \(\displaystyle \delta\) szögére és a vele szemben levő \(\displaystyle NE\) oldalra felírt koszinusztétel segítségével megállapíthatjuk, hogy \(\displaystyle x=1\) esetén \(\displaystyle \delta=135^{\circ}\) és \(\displaystyle x=6\) esetén \(\displaystyle \delta=45^{\circ}\).
2. megoldás. Felhasználjuk az 1. megoldás ábrájának jelöléseit és azt az eredményt, hogy a \(\displaystyle DNE\) háromszögben \(\displaystyle EDN\sphericalangle=\delta\), illetve azt, hogy \(\displaystyle AN=3\) és \(\displaystyle AE=2\).
Felírjuk a \(\displaystyle DNA\) és \(\displaystyle DEA\) háromszögekben a \(\displaystyle D\) csúcshoz tartozó hegyesszögek tangensét:
\(\displaystyle \displaystyle{\tg{NDA\sphericalangle}=\frac{3}{x};\quad \tg{EDA\sphericalangle}=\frac{2}{x}}.\)
Mivel \(\displaystyle \delta=NDA\sphericalangle+EDA\sphericalangle\), alkalmazhatjuk a \(\displaystyle \delta\) szögre a
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\tg{\delta}=\frac{\frac{2}{x}+\frac{3}{x}}{1-\frac{2}{x}\cdot{\frac{3}{x}}}}\) |
trigonometrikus addíciós tételt.
Ha \(\displaystyle \delta=45^{\circ}\), akkor \(\displaystyle \tg45^{\circ}=1\) miatt az (1) egyenletből egyszerű átalaításokkal az \(\displaystyle x^2-5x-6=0\) egyenletet kapjuk. Ennek egyetlen pozitív megoldása \(\displaystyle x=6\).
Ha pedig \(\displaystyle \delta=135^{\circ}\), akkor \(\displaystyle \tg135^{\circ}=-1\) miatt az (1) egyenletből az \(\displaystyle x^2+5x-6=0\) másodfokú egyenletet kapjuk, amelynek egyetlen pozitív megoldása \(\displaystyle x=1\).
A feladat feltételei mellett tehát az \(\displaystyle ABCD\) négyzet oldalainak hossza \(\displaystyle \delta=45^{\circ}\) esetén \(\displaystyle x=6\), \(\displaystyle \delta=135^{\circ}\) esetén pedig \(\displaystyle x=1\).
3. megoldás. Felhasználjuk az 1. megoldás ábrájának jelöléseit és azt az eredményt, hogy a \(\displaystyle DNE\) háromszögben \(\displaystyle EDN\sphericalangle=\delta\), \(\displaystyle DNE\sphericalangle=\varphi\), illetve
\(\displaystyle \displaystyle{DN=\sqrt{x^2+9}; \quad DE=\sqrt{x^2+4}}.\)
Legyen először \(\displaystyle \delta=45^{\circ}\) és tekintsük a következő ábrát.
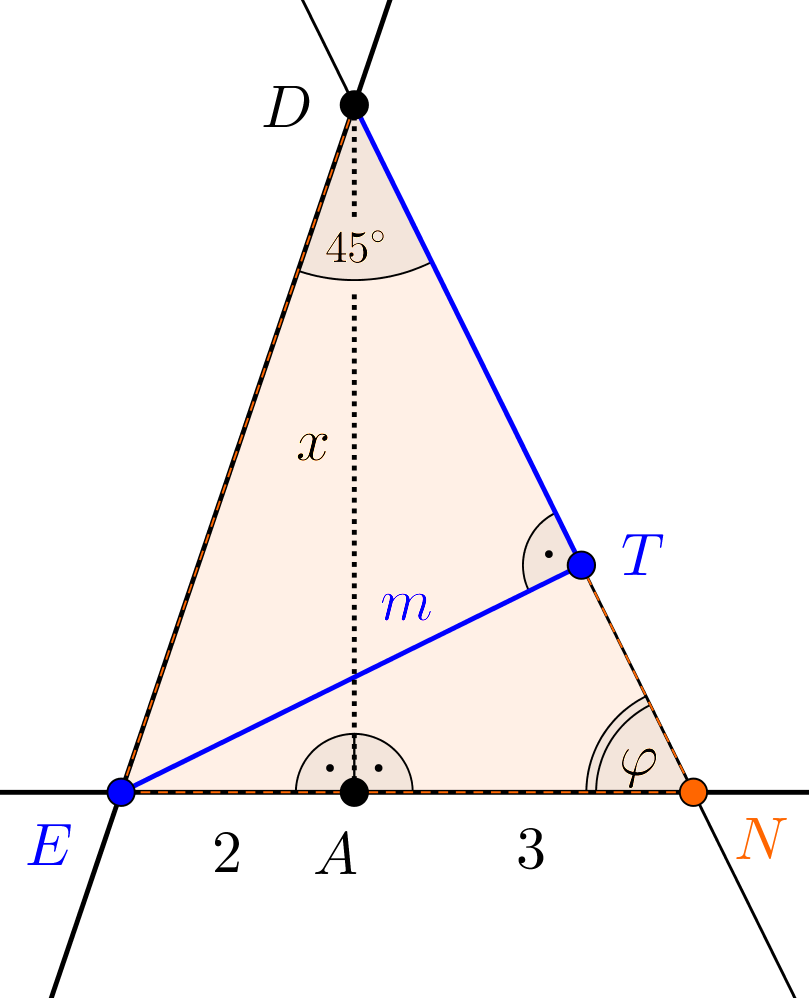
A \(\displaystyle DNE\) háromszög \(\displaystyle E\) pontjából a \(\displaystyle DN\)-re bocsátott merőleges talppontját \(\displaystyle T\)-vel jelöltük. Az \(\displaystyle ET=m\) szakasz a háromszög \(\displaystyle E\)-ből húzott magassága.
A \(\displaystyle DET\) háromszög nyilvánvalóan egyenlő szárú derékszögű háromszög, ezért \(\displaystyle DT=m\) és \(\displaystyle DE=m\cdot{\sqrt{2}}\), azaz
| \(\displaystyle (1)\) | \(\displaystyle \sqrt{x^2+4}=m\cdot{\sqrt{2}}.\) |
A \(\displaystyle DNE\) háromszög kétszeres területét kétféleképpen is felírhatjuk: \(\displaystyle DN\cdot m=NE\cdot x\), vagyis
\(\displaystyle \sqrt{x^2+9}\cdot m= 5\cdot x,\)
innen (1) alapján
| \(\displaystyle (2)\) | \(\displaystyle \sqrt{x^2+9}\cdot{\sqrt{x^2+4}}=5\sqrt{2}\cdot x.\) |
Legyen most \(\displaystyle \delta=135^{\circ}\) és vizsgáljuk az ennek megfelelően készített ábrát, amelyen most is megrajzoltuk a \(\displaystyle DNE\) háromszög \(\displaystyle E\) csúcsból húzott magasságát.
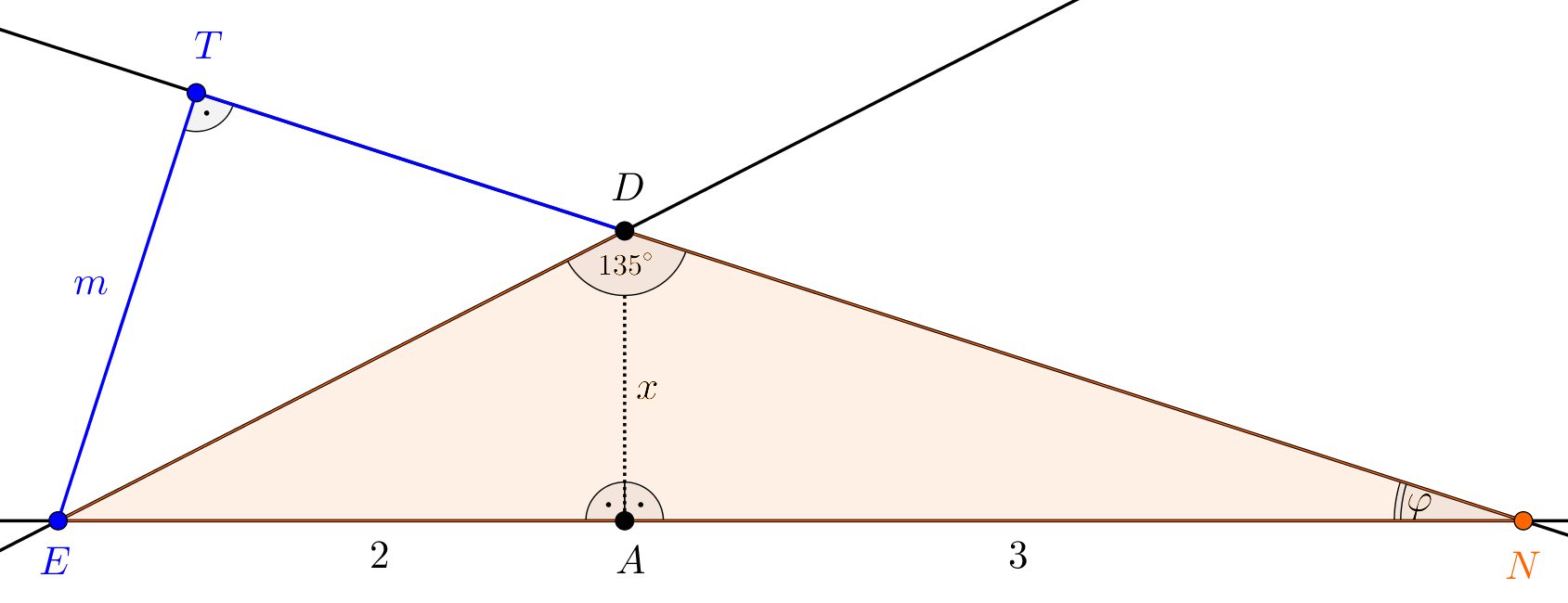
A \(\displaystyle DET\) derékszögű háromszög ezúttal is egyenlő szárú, hiszen \(\displaystyle EDT\sphericalangle=45^{\circ}\), és így \(\displaystyle DET\sphericalangle=45^{\circ}\).
Ez azt jelenti, hogy ismét felírható az (1) egyenlet és a \(\displaystyle DNE\) háromszög kétszeres területére kapott
\(\displaystyle \sqrt{x^2+9}\cdot m= 5\cdot x\)
összefüggés, ahonnan egyszerű átalakítással újra a (2) egyenlethez jutunk.
Ez azt jelenti, hogy a \(\displaystyle \delta=45^{\circ}\) és a \(\displaystyle \delta=135^{\circ}\) esetén is ugyanazt a
\(\displaystyle \sqrt{x^2+9}\cdot{\sqrt{x^2+4}}=5\sqrt{2}\cdot x\)
egyenletet kapjuk.
Az egyenlet mindkét oldalának négyzetre emelésével és rendezéssel (az 1. megoldásban is látott)
\(\displaystyle x^4-37x^2+36=0\)
egyenlet adódik, ahonnan \(\displaystyle x^2=1\) és \(\displaystyle x^2=36\), innen pedig az egyenlet pozitív megoldásai \(\displaystyle x=1\) és \(\displaystyle x=6\).
Ezek tehát az \(\displaystyle ABCD\) négyzet oldalának lehetséges értékei.
A \(\displaystyle DNE\) háromszög \(\displaystyle \delta\) szögére és a vele szemben levő \(\displaystyle NE\) oldalra felírt koszinusztétel segítségével ezúttal is ellenőrizhetjük, hogy az \(\displaystyle x=1\) értékhez \(\displaystyle \delta=135^{\circ}\), az \(\displaystyle x=6\) értékhez pedig \(\displaystyle \delta=45^{\circ}\) tartozik.
Statistics:
32 students sent a solution. 5 points: Baksa Anna, Braun Zsófia, Fiser 234 Boldizsár, Hajós Balázs, Hetényi Klára Tímea, Keszthelyi Eszter, Petró Péter, Richlik Márton, Schneider Dávid. 4 points: Emődi Marcell, Fekete Patrik, Hosszu Noel, Mészáros Anna Veronika, Sipeki Márton, Szittyai Anna, Végh Lilian. 3 points: 5 students. 2 points: 1 student. 1 point: 2 students. 0 point: 2 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, December 2022
