 |
A C. 1746. feladat (2022. december) |
C. 1746. Az \(\displaystyle ABCD\) négyzet \(\displaystyle AB\) oldalát az \(\displaystyle A\) ponton túl meghosszabbítjuk az \(\displaystyle AE=2\) szakasszal, a \(\displaystyle B\) ponton túl pedig a \(\displaystyle BF=3\) szakasszal. Az \(\displaystyle ED\) és \(\displaystyle FC\) egyenesek \(\displaystyle 45^{\circ}\)-os szöget zárnak be. Határozzuk meg a négyzet oldalának lehetséges értékeit.
Javasolta: Németh László (Fonyód)
(5 pont)
A beküldési határidő 2023. január 10-én LEJÁRT.
1. megoldás. Legyen az \(\displaystyle ABCD\) négyzet oldalának hossza \(\displaystyle x\), az \(\displaystyle ED\) és \(\displaystyle FC\) egyenesek metszéspontja \(\displaystyle M\). Ha az egyenesek \(\displaystyle 45^{\circ}\)-os szöget zárnak be, akkor két eset lehetséges: \(\displaystyle EMF\sphericalangle=45^{\circ}\), vagy \(\displaystyle EMF\sphericalangle=135^{\circ}\). Húzzunk párhuzamost a \(\displaystyle D\) ponton keresztül az \(\displaystyle MF\) egyenessel, ez az \(\displaystyle AB\) egyenesét az \(\displaystyle N\) pontban metszi.
Tekintsük az alábbi vázlatos ábrát, amelyen \(\displaystyle EMF\sphericalangle=\delta\) és \(\displaystyle MFE\sphericalangle=\varphi\).
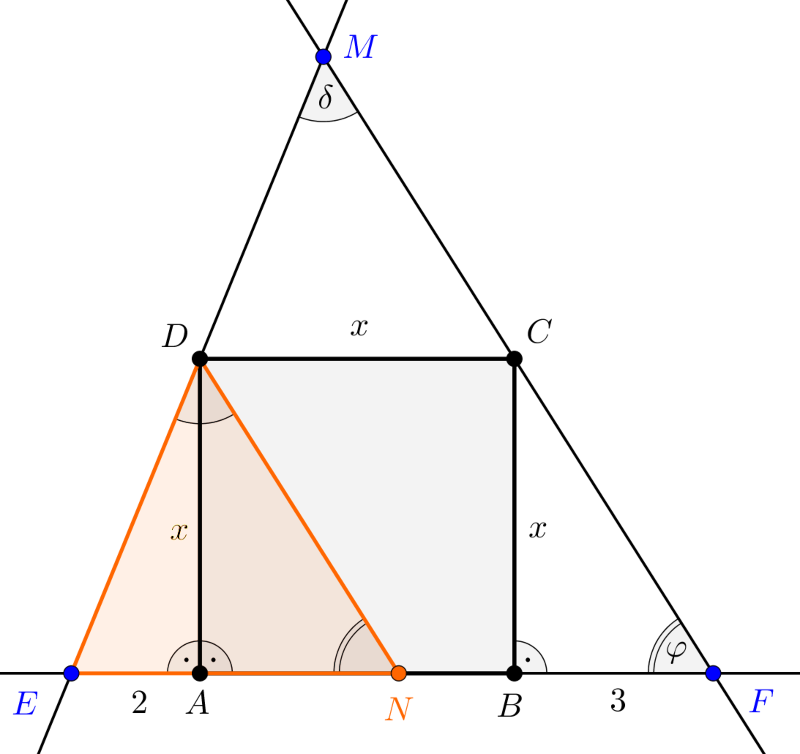
Mivel \(\displaystyle CD\parallel{AB}\) és \(\displaystyle CF\parallel{DN}\), ezért egyrészt \(\displaystyle CDNF\) paralelogramma, és így \(\displaystyle CF=DN\), másrészt \(\displaystyle DNA\sphericalangle\) és \(\displaystyle CFB\sphericalangle\) egyállású szögek, tehát egyenlők, azaz \(\displaystyle DNA\sphericalangle=\varphi\).
A \(\displaystyle DNA\) és \(\displaystyle CFB\) háromszögek szögei egyenlő nagyságúak és mivel a két háromszögben \(\displaystyle CF=DN\), ezért a két háromszög egybevágó, emiatt \(\displaystyle AN=3\).
A \(\displaystyle DNA\) és \(\displaystyle DEA\) derékszögű háromszögekre felírt Pitagorasz-tételekből következik, hogy
\(\displaystyle \displaystyle{DN=\sqrt{x^2+9}; \quad DE=\sqrt{x^2+4}}.\)
A \(\displaystyle DNA\) háromszögben \(\displaystyle DNA\sphericalangle=\varphi\), ezért
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\sin{\varphi}=\frac{DA}{DN}=\frac{x}{\sqrt{x^2+9}}}.\) |
Ugyanakkor a \(\displaystyle DN\) és \(\displaystyle MF\) párhuzamosságából az is következik, hogy \(\displaystyle EDN\sphericalangle=\delta\), és ezért \(\displaystyle \sin{EDN\sphericalangle}=\sin{\delta}\).
A feltételek miatt \(\displaystyle \delta=45^{\circ}\) vagy \(\displaystyle \delta=135^{\circ}\), ezért
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\sin{\delta}=\sin{45^{\circ}}=\sin{135^{\circ}}=\frac{\sqrt{2}}{2}}.\) |
Felírjuk a szinusztételt a \(\displaystyle DNE\) háromszögben:
\(\displaystyle \displaystyle{\frac{DE}{NE}=\frac{\sin{\varphi}}{\sin{\delta}}},\)
ebből \(\displaystyle DE=\sqrt{x^2+4}\) és \(\displaystyle NE=5\), illetve (1), valamint (2) alapján
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{\frac{\sqrt{x^2+4}}{5}=\frac{\frac{x}{\sqrt{x^2+9}}}{\frac{\sqrt{2}}{2}}}\) |
következik.
A (3) egyenletből négyzetreemelés és a műveletek elvégzése után \(\displaystyle \big(x^2+4\big)\cdot\big(x^2+9\big)=50x^2\), innen pedig
| \(\displaystyle (4)\) | \(\displaystyle x^4-37x^2+36=0\) |
adódik.
A (4) egyenletből \(\displaystyle x^2\) értékére két megoldást kapunk: \(\displaystyle x^2=1\) és \(\displaystyle x^2=36\).
Az \(\displaystyle x\) csak pozitív szám lehet, ezért az \(\displaystyle ABCD\) négyzet oldalhosszának értéke \(\displaystyle x=1\) és \(\displaystyle x=6\) lehet.
Trigonometriai úton, például a \(\displaystyle DNE\) háromszög \(\displaystyle \delta\) szögére és a vele szemben levő \(\displaystyle NE\) oldalra felírt koszinusztétel segítségével megállapíthatjuk, hogy \(\displaystyle x=1\) esetén \(\displaystyle \delta=135^{\circ}\) és \(\displaystyle x=6\) esetén \(\displaystyle \delta=45^{\circ}\).
2. megoldás. Felhasználjuk az 1. megoldás ábrájának jelöléseit és azt az eredményt, hogy a \(\displaystyle DNE\) háromszögben \(\displaystyle EDN\sphericalangle=\delta\), illetve azt, hogy \(\displaystyle AN=3\) és \(\displaystyle AE=2\).
Felírjuk a \(\displaystyle DNA\) és \(\displaystyle DEA\) háromszögekben a \(\displaystyle D\) csúcshoz tartozó hegyesszögek tangensét:
\(\displaystyle \displaystyle{\tg{NDA\sphericalangle}=\frac{3}{x};\quad \tg{EDA\sphericalangle}=\frac{2}{x}}.\)
Mivel \(\displaystyle \delta=NDA\sphericalangle+EDA\sphericalangle\), alkalmazhatjuk a \(\displaystyle \delta\) szögre a
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\tg{\delta}=\frac{\frac{2}{x}+\frac{3}{x}}{1-\frac{2}{x}\cdot{\frac{3}{x}}}}\) |
trigonometrikus addíciós tételt.
Ha \(\displaystyle \delta=45^{\circ}\), akkor \(\displaystyle \tg45^{\circ}=1\) miatt az (1) egyenletből egyszerű átalaításokkal az \(\displaystyle x^2-5x-6=0\) egyenletet kapjuk. Ennek egyetlen pozitív megoldása \(\displaystyle x=6\).
Ha pedig \(\displaystyle \delta=135^{\circ}\), akkor \(\displaystyle \tg135^{\circ}=-1\) miatt az (1) egyenletből az \(\displaystyle x^2+5x-6=0\) másodfokú egyenletet kapjuk, amelynek egyetlen pozitív megoldása \(\displaystyle x=1\).
A feladat feltételei mellett tehát az \(\displaystyle ABCD\) négyzet oldalainak hossza \(\displaystyle \delta=45^{\circ}\) esetén \(\displaystyle x=6\), \(\displaystyle \delta=135^{\circ}\) esetén pedig \(\displaystyle x=1\).
3. megoldás. Felhasználjuk az 1. megoldás ábrájának jelöléseit és azt az eredményt, hogy a \(\displaystyle DNE\) háromszögben \(\displaystyle EDN\sphericalangle=\delta\), \(\displaystyle DNE\sphericalangle=\varphi\), illetve
\(\displaystyle \displaystyle{DN=\sqrt{x^2+9}; \quad DE=\sqrt{x^2+4}}.\)
Legyen először \(\displaystyle \delta=45^{\circ}\) és tekintsük a következő ábrát.
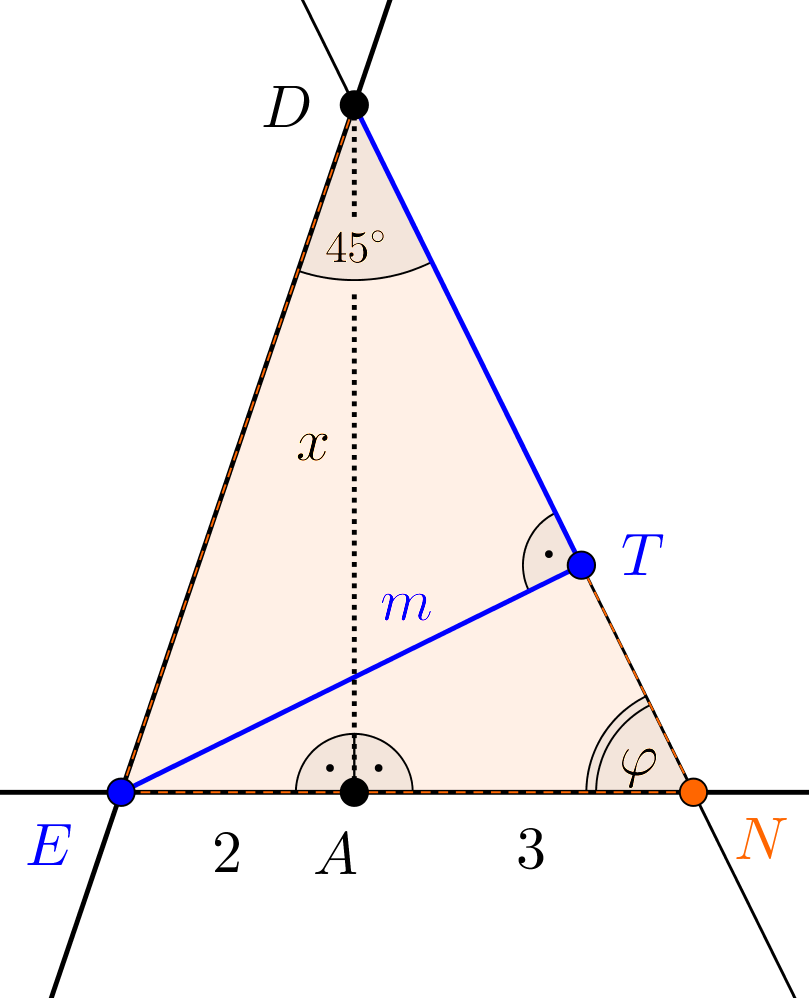
A \(\displaystyle DNE\) háromszög \(\displaystyle E\) pontjából a \(\displaystyle DN\)-re bocsátott merőleges talppontját \(\displaystyle T\)-vel jelöltük. Az \(\displaystyle ET=m\) szakasz a háromszög \(\displaystyle E\)-ből húzott magassága.
A \(\displaystyle DET\) háromszög nyilvánvalóan egyenlő szárú derékszögű háromszög, ezért \(\displaystyle DT=m\) és \(\displaystyle DE=m\cdot{\sqrt{2}}\), azaz
| \(\displaystyle (1)\) | \(\displaystyle \sqrt{x^2+4}=m\cdot{\sqrt{2}}.\) |
A \(\displaystyle DNE\) háromszög kétszeres területét kétféleképpen is felírhatjuk: \(\displaystyle DN\cdot m=NE\cdot x\), vagyis
\(\displaystyle \sqrt{x^2+9}\cdot m= 5\cdot x,\)
innen (1) alapján
| \(\displaystyle (2)\) | \(\displaystyle \sqrt{x^2+9}\cdot{\sqrt{x^2+4}}=5\sqrt{2}\cdot x.\) |
Legyen most \(\displaystyle \delta=135^{\circ}\) és vizsgáljuk az ennek megfelelően készített ábrát, amelyen most is megrajzoltuk a \(\displaystyle DNE\) háromszög \(\displaystyle E\) csúcsból húzott magasságát.
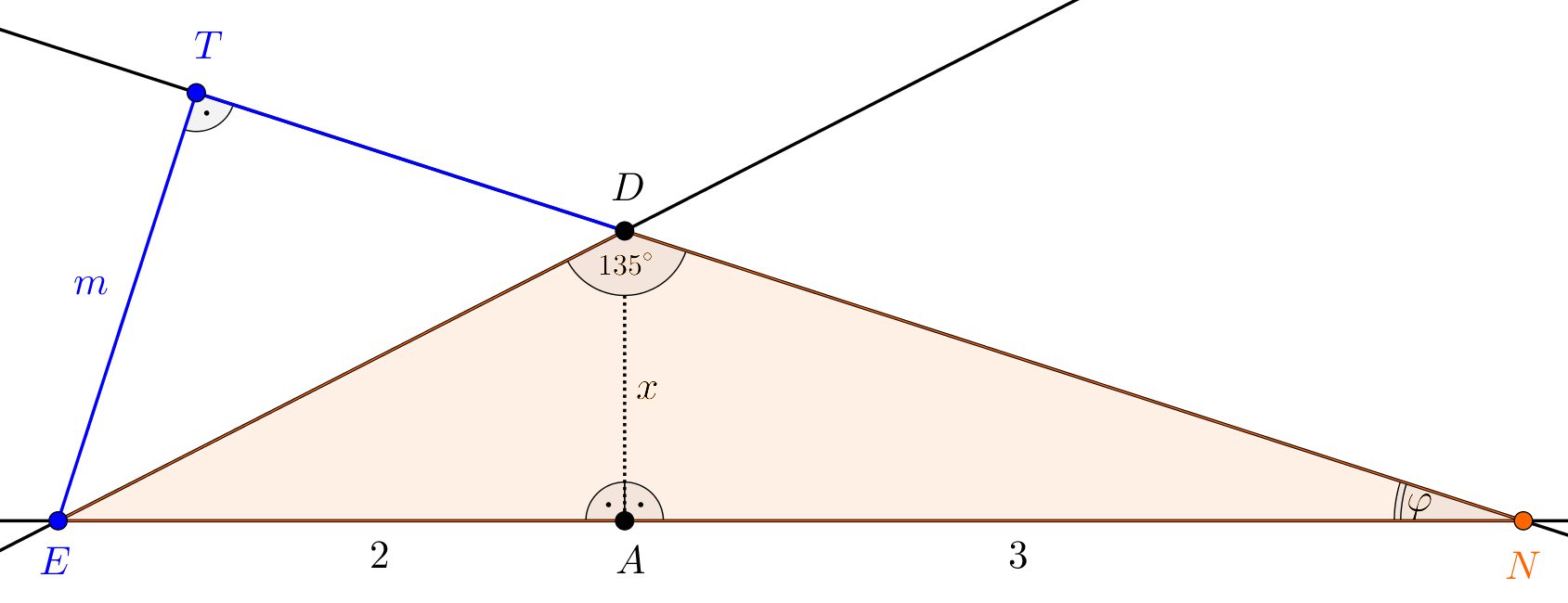
A \(\displaystyle DET\) derékszögű háromszög ezúttal is egyenlő szárú, hiszen \(\displaystyle EDT\sphericalangle=45^{\circ}\), és így \(\displaystyle DET\sphericalangle=45^{\circ}\).
Ez azt jelenti, hogy ismét felírható az (1) egyenlet és a \(\displaystyle DNE\) háromszög kétszeres területére kapott
\(\displaystyle \sqrt{x^2+9}\cdot m= 5\cdot x\)
összefüggés, ahonnan egyszerű átalakítással újra a (2) egyenlethez jutunk.
Ez azt jelenti, hogy a \(\displaystyle \delta=45^{\circ}\) és a \(\displaystyle \delta=135^{\circ}\) esetén is ugyanazt a
\(\displaystyle \sqrt{x^2+9}\cdot{\sqrt{x^2+4}}=5\sqrt{2}\cdot x\)
egyenletet kapjuk.
Az egyenlet mindkét oldalának négyzetre emelésével és rendezéssel (az 1. megoldásban is látott)
\(\displaystyle x^4-37x^2+36=0\)
egyenlet adódik, ahonnan \(\displaystyle x^2=1\) és \(\displaystyle x^2=36\), innen pedig az egyenlet pozitív megoldásai \(\displaystyle x=1\) és \(\displaystyle x=6\).
Ezek tehát az \(\displaystyle ABCD\) négyzet oldalának lehetséges értékei.
A \(\displaystyle DNE\) háromszög \(\displaystyle \delta\) szögére és a vele szemben levő \(\displaystyle NE\) oldalra felírt koszinusztétel segítségével ezúttal is ellenőrizhetjük, hogy az \(\displaystyle x=1\) értékhez \(\displaystyle \delta=135^{\circ}\), az \(\displaystyle x=6\) értékhez pedig \(\displaystyle \delta=45^{\circ}\) tartozik.
Statisztika:
32 dolgozat érkezett. 5 pontot kapott: Baksa Anna, Braun Zsófia, Fiser 234 Boldizsár, Hajós Balázs, Hetényi Klára Tímea, Keszthelyi Eszter, Petró Péter, Richlik Márton, Schneider Dávid. 4 pontot kapott: Emődi Marcell, Fekete Patrik, Hosszu Noel, Mészáros Anna Veronika, Sipeki Márton, Szittyai Anna, Végh Lilian. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2022. decemberi matematika feladatai

