 |
A C. 1750. feladat (2023. január) |
C. 1750. Az \(\displaystyle O_1\) középpontú \(\displaystyle k_1\) és az \(\displaystyle O_2\) középpontú \(\displaystyle k_2\) körök közös pontjai \(\displaystyle M\) és \(\displaystyle N\). Az \(\displaystyle M\) ponton áthaladó szelő a \(\displaystyle k_1\) kört az \(\displaystyle A\), a \(\displaystyle k_2\) kört a \(\displaystyle B\) pontban metszi úgy, hogy \(\displaystyle A\) a \(\displaystyle k_2\) körre, \(\displaystyle B\) a \(\displaystyle k_1\) körre nézve külső pont. Az \(\displaystyle AO_1\) és \(\displaystyle BO_2\) egyenesek közös pontja \(\displaystyle P\). Az \(\displaystyle N\) és a \(\displaystyle P\) pont az \(\displaystyle O_1O_2\) egyenes által meghatározott két félsík közül ugyanabba esik. Mutassuk meg, hogy \(\displaystyle P\) illeszkedik az \(\displaystyle O_1NO_2\) háromszög körülírt körére.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2023. február 10-én LEJÁRT.
Megoldás. A feltétel miatt az \(\displaystyle A\) és \(\displaystyle B\) pontok nem lehetnek azonosak sem az \(\displaystyle M\), sem az \(\displaystyle N\) ponttal, továbbá \(\displaystyle A\) nem illeszkedhet a \(\displaystyle k_1\) körnek a \(\displaystyle k_2\) kör belső pontjaiból álló \(\displaystyle MN\) körívére, hasonlóképpen \(\displaystyle B\) nem lehet a \(\displaystyle k_2\) kör azon \(\displaystyle MN\) körívén, amelyet a \(\displaystyle k_1\) kör belső pontjai alkotnak.
Az \(\displaystyle M\) és \(\displaystyle N\) pontok nyilvánvalóan az \(\displaystyle O_1O_2\) egyenes által meghatározott különböző félsíkokban vannak, így a feltétel szerint \(\displaystyle P\) és \(\displaystyle M\) is az így létrejövő különböző félsíkokba esnek.
Legyen az \(\displaystyle O_1NO_2\) háromszögben \(\displaystyle O_2O_1N\sphericalangle=\alpha\) és \(\displaystyle NO_2O_1\sphericalangle=\beta\). Az \(\displaystyle O_1O_2\) szakasznak az \(\displaystyle N\) pontból mért látószöge nyilvánvaló, hogy
| \(\displaystyle (1)\) | \(\displaystyle \varphi=180^{\circ}-\alpha-\beta.\) |
Mivel \(\displaystyle P\) és \(\displaystyle N\) azonos félsíkban vannak, ezért \(\displaystyle P\) pontosan akkor illeszkedik az \(\displaystyle O_1NO_2\) háromszög körülírt körére, ha a \(\displaystyle P\) pontból az \(\displaystyle O_1O_2\) szakasz az (1) összefüggésben szereplő
\(\displaystyle \displaystyle{\varphi=180^{\circ}-\alpha-\beta}\)
szögben látszik.
Azt fogjuk bizonyítani, hogy az \(\displaystyle AB\) szelő bármely, a feltételnek megfelelő választása esetén az \(\displaystyle AB\) szakasz az \(\displaystyle N\) pontból az (1) alatti \(\displaystyle \varphi\) szögben látszik, ebből következni fog a feladat állítása.
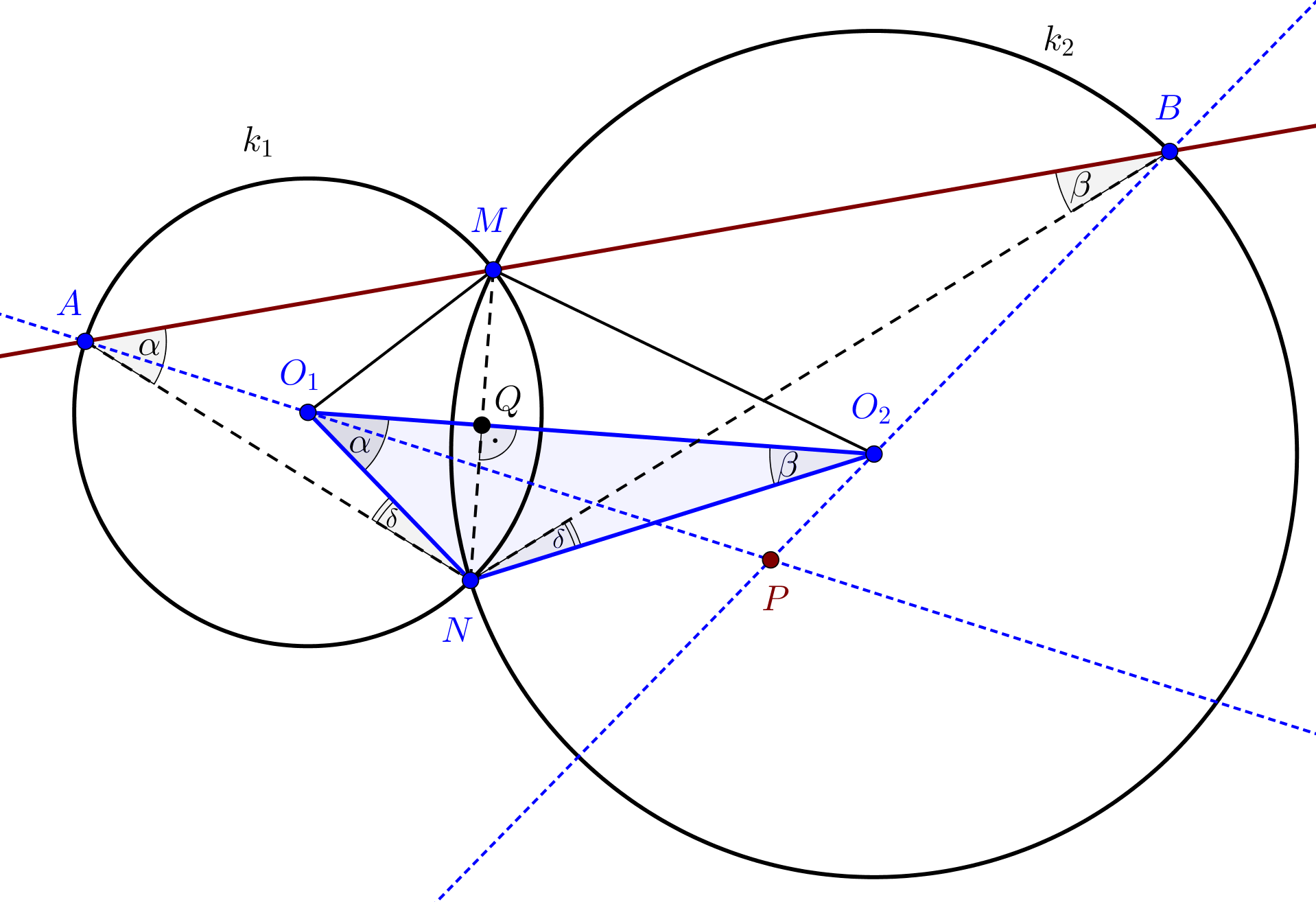
Tekintsük az 1. ábrát.
1. ábra
Nyilvánvaló, hogy \(\displaystyle O_1M=O_1N\), illetve \(\displaystyle O_2M=O_2N\), továbbá az \(\displaystyle O_1NO_2\) és \(\displaystyle O_1MO_2\) háromszögekben \(\displaystyle O_1O_2\) közös, ezért ezek a háromszögek egybevágók. Ez azt is jelenti, hogy \(\displaystyle MO_1O_2\sphericalangle=\alpha\) és \(\displaystyle MO_2O_1\sphericalangle=\beta\).
Ekkor \(\displaystyle MO_1N\sphericalangle=2\alpha\), valamint \(\displaystyle MO_2N\sphericalangle=2\beta\), és így a középponti és kerületi szögek közötti összefüggés szerint a \(\displaystyle k_1\) körben \(\displaystyle MAN\sphericalangle=\alpha\), a \(\displaystyle k_2\) körben \(\displaystyle MBN\sphericalangle=\beta\). Ezzel igazoltuk, hogy \(\displaystyle ANB\sphericalangle=180^{\circ}-\alpha-\beta\), tehát az \(\displaystyle AB\) szakasz az \(\displaystyle N\) pontból valóban \(\displaystyle \varphi\) szög alatt látszik.
Eredményünk szerint az \(\displaystyle O_1NO_2\) és \(\displaystyle ANB\) háromszögek hasonlók, mert megfelelő szögeik egyenlők. Ez azt jelenti, hogy a háromszögek \(\displaystyle N\) középpontú forgatva nyújtással átvihetők egymásba.
Jelöljük az elforgatás szögét \(\displaystyle \delta\)-val. Az 1.ábrán az \(\displaystyle O_1AN\) egyenlő szárú háromszögben \(\displaystyle O_1NA\sphericalangle=O_1AN\sphericalangle=\delta\), az \(\displaystyle O_2NB\) egyenlő szárú háromszögben pedig \(\displaystyle O_2NB\sphericalangle=O_2BN\sphericalangle=\delta\), ebből az következik, hogy \(\displaystyle BAP\sphericalangle+ABP\sphericalangle=\alpha+\beta\), ezért a \(\displaystyle P\) pontból az \(\displaystyle AB\), ezzel együtt az \(\displaystyle O_1O_2\) szakasz is
\(\displaystyle \varphi=180^{\circ}-\alpha-\beta\)
szögben látszik.
Ez éppen azt jelenti, hogy az azonos félsíkban levő \(\displaystyle P\), \(\displaystyle N\) pontok rajta vannak az \(\displaystyle O_1O_2\) szakasz fölé rajzolt \(\displaystyle \varphi\) szögű látószögköríven, ezért \(\displaystyle P\) illeszkedik az \(\displaystyle O_1NO_2\) háromszög körülírt körére. Ezzel a feladat állítását bizonyítottuk.
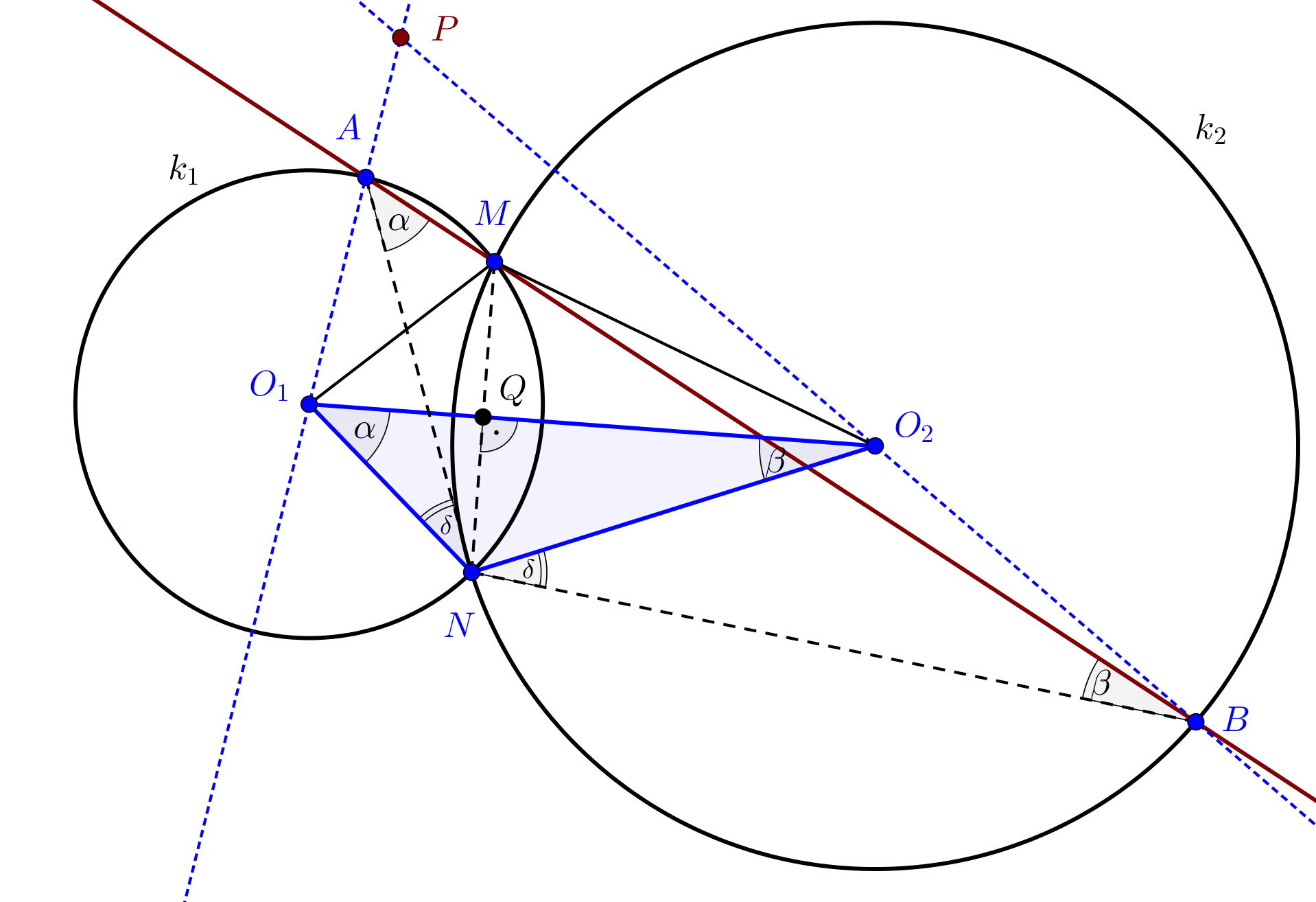
Megjegyzések. 1) Könnyen bizonyíthatjuk, hogy a feladat állítása abban az esetben is teljesül, ha a \(\displaystyle P\), \(\displaystyle N\) pontok az \(\displaystyle O_1O_2\) által létrehozott különböző félsíkokban vannak. Ehhez tekintsük a 2. ábrát.
2. ábra
A megoldásban leírtakhoz teljesen hasonló módon igazolható, hogy az \(\displaystyle O_1NO_2\) és \(\displaystyle ANB\) háromszögek hasonlók, tehát a két háromszög ismét átvihető egymásba egy \(\displaystyle N\) középpontú forgatva nyújtással, az elforgatás szögét ismét \(\displaystyle \delta\)-val jelöljük.. A 2.ábrán az \(\displaystyle O_1AN\) egyenlő szárú háromszögben \(\displaystyle O_1NA\sphericalangle=O_1AN\sphericalangle=\delta\), az \(\displaystyle O_2NB\) egyenlő szárú háromszögben pedig \(\displaystyle O_2NB\sphericalangle=O_2BN\sphericalangle=\delta\).
Eszerint
| \(\displaystyle (2)\) | \(\displaystyle BAO_1\sphericalangle=\alpha+\delta;\quad {ABP\sphericalangle=\delta-\beta}.\) |
A \(\displaystyle BAO_1\sphericalangle\) külső szöge az \(\displaystyle ABP\) háromszögnek, ezért \(\displaystyle BAO_1\sphericalangle=BPA\sphericalangle+ABP\sphericalangle\), így (2) alapján azt kapjuk, hogy \(\displaystyle \alpha+\delta=BPA\sphericalangle+\delta-\beta\), azaz \(\displaystyle BPA\sphericalangle=\alpha+\beta\). A kapott összefüggés szerint teljesül az is, hogy
| \(\displaystyle (3)\) | \(\displaystyle O_2PO_1\sphericalangle=\alpha+\beta=180^{\circ}-\varphi.\) |
A (3) egyenlőség azt jelenti, hogy az \(\displaystyle O_1NO_2P\) négyszögben az \(\displaystyle N\) és \(\displaystyle P\) csúcsoknál levő belső szögek összege \(\displaystyle 180^{\circ}\), tehát a négyszög húrnégyszög. Ebből pedig azonnal adódik, hogy \(\displaystyle P\) illeszkedik \(\displaystyle O_1NO_2\) háromszög körülírt körére.
2) Ha a megoldásban leírt forgatva nyújtásnál az elforgatás szögére \(\displaystyle \delta=0^{\circ}\) áll fenn, akkor az \(\displaystyle O_1NO_2\) és \(\displaystyle ANB\) háromszögek egyszerű középpontos hasonlóságáról van szó. Ebben az esetben a \(\displaystyle P\) és \(\displaystyle N\) pontok azonosak, a feladat állítása ekkor nyilvánvalóan teljesül.
Az \(\displaystyle AB\) szelő speciális elhelyezkedése esetén előfordulhat, hogy \(\displaystyle P=A\), illetve \(\displaystyle P=B\). Az előbbi akkor valósulhat meg, ha az \(\displaystyle AB\) egyenes áthalad az \(\displaystyle O_2\) ponton, míg az utóbbi akkor, ha az \(\displaystyle AB\) egyenesre illeszkedik az \(\displaystyle O_1\) pont. A feladat állítása mindkét esetben a fentiekben követett gondolatmenettel igazolható.
3) A feladat állítása akkor is könnyen bizonyítható, ha nem kötjük ki, hogy \(\displaystyle A\) a \(\displaystyle k_2\) körre, \(\displaystyle B\) a \(\displaystyle k_1\) körre nézve külső pont.
4) Az az állítás, hogy az \(\displaystyle AB\) szelő bármely választása esetén az \(\displaystyle AB\) szakasz az \(\displaystyle N\) pontból mindig ugyanakkora szögben látszik, a Geometriai feladatgyűjtemény I. kötetének 1022. feladata.
Statisztika:
73 dolgozat érkezett. 5 pontot kapott: Aaishipragya Kahaly, Beke Botond, Biborka Bernadett, Dózsa-Kovács Leonárd, Fiser 234 Boldizsár, Gáthi Donát, Halász Henrik, Hosszu Noel, Iván Máté Domonkos, Kerekes András, Keszthelyi Eszter, Klement Tamás, Kovács Barnabás, Kővágó Edit Gréta, Kriston Nándor, Sipeki Márton, Somogyi Dóra, Sütő Áron, Székely Márton, Teveli Jakab, Török Eszter Júlia, Ujpál Bálint, Waldhauser Miklós. 4 pontot kapott: Barna Márton, Egyházi Godó, Fekete Patrik, Forrai Boldizsár, Gyenes Károly, Kovács Dániel, Németh Hanna Júlia , Szabó Donát, Tömböly 299 Áron. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 20 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2023. januári matematika feladatai
