Problem C. 1757. (February 2023)

C. 1757. Johnny got a robot for Christmas, and he is trying it on a square carpet. The length of the sides of the square is \(\displaystyle 4\) metres, and its vertices are \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) and \(\displaystyle D\), in this order. Let \(\displaystyle P\) denote the interior point of square \(\displaystyle ABCD\) which is exactly \(\displaystyle 1\) metre away from both of sides \(\displaystyle AB\) and \(\displaystyle BC\). The robot is initially standing at point \(\displaystyle P\), and starts to move in a random direction. When it has covered \(\displaystyle 2\) metres, it will stop. What is the probability that the robot will get off the carpet?

Proposed by K.\(\displaystyle \,\)A. Kozma, Győr

(5 pont)

Deadline expired on March 10, 2023.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Készítsünk ábrát és használjuk annak jelöléseit.

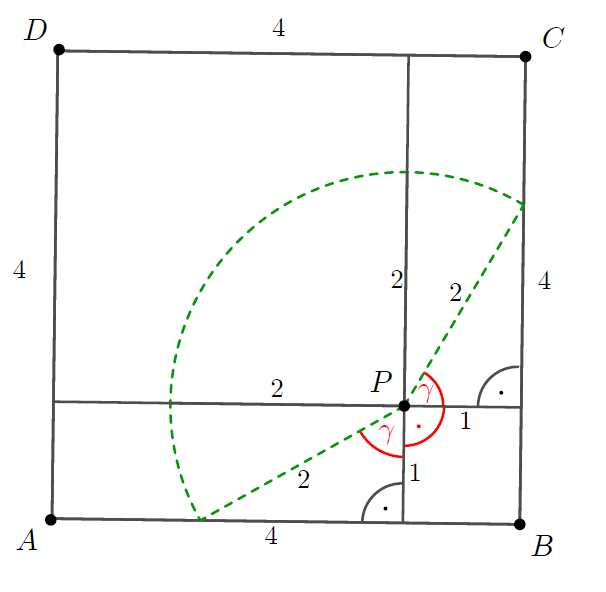
Jelöljük be a \(\displaystyle P\) középpontú, \(\displaystyle 2\) egység sugarú körvonal azon pontjait, amelyek az \(\displaystyle ABCD\) négyzeten belül vagy annak kerületén vannak. Ha a robot a megjelölt pontok valamelyikébe érkezik, akkor a szőnyegen marad, minden más esetben a szőnyegen kívül lesz. A valószínűség kiszámítására a geometriai modellt alkalmazva az eseménytér mértéke a teljesszög nagysága, amely \(\displaystyle 360^{\circ}\). A robot pontosan akkor lesz a szőnyegen kívül, ha a szaggatott körcikken kívül megy: azaz vagy a két bejelölt \(\displaystyle \gamma\) nagyságú szögtartományban, vagy a kis négyzet belsejében halad. Ezért a megfelelő szögtartomány nagysága összesen \(\displaystyle 2\gamma + 90^{\circ}\). A \(\displaystyle \gamma\) szöget tartalmazó derékszögű háromszög oldalhosszainak ismeretében meghatározzuk a szög koszinuszát: \(\displaystyle \cos \gamma= \frac{1}{2}\), amelyből megkapjuk a szög nagyságát: \(\displaystyle \gamma =60^{\circ}\). A kérdezett valószínűség

\(\displaystyle p=\frac{2 \cdot 60^{\circ}+90^{\circ} }{360^{\circ}}=\frac{7}{12}\hbox{.}\)

Statistics:

41 students sent a solution.
5 points:	Bezsilla Gábor, Bóta Bálint, Braun Zsófia, Buris Orsolya, Fiser 234 Boldizsár, Heltovics Lilla, Ispán Bence, Jójárt Emese, Keszthelyi Eszter, Mészáros Anna Veronika, Petró Péter, Réz Petra, Richlik Márton, Seprődi Barnabás Bendegúz, Sipeki Márton, Szegedi Ágoston, Szittyai Anna, Varga 241 Ildikó Kata, Varga Dániel 829, Végh Lilian, Waldhauser Miklós.
4 points:	Csorba Mihály, Fekete Patrik, Hosszu Noel, Hüvös Gergely, Josepovits Gábor, Juhász 119 Áron, Rigó Bálint, Schneider Dávid, Tomesz László Gergő, Varga 621 Emese .
3 points:	3 students.
2 points:	2 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, February 2023