 Problem C. 1771. (May 2023)
Problem C. 1771. (May 2023)
C. 1771. In isosceles right-angled triangle \(\displaystyle ABC\), the midpoint of leg \(\displaystyle BC\) is \(\displaystyle D\), and the point closer to vertex \(\displaystyle B\) that divides the hypotenuse in a one to two ratio is \(\displaystyle E\). Prove that \(\displaystyle AD\) and \(\displaystyle CE\) are perpendicular.
Proposed by B. Bíró, Eger
(5 pont)
Deadline expired on June 12, 2023.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Legyen az \(\displaystyle ABC\) háromszög befogóinak hossza \(\displaystyle a\), ekkor az \(\displaystyle AB\) átfogó hossza \(\displaystyle a\sqrt{2}\). Tekintsük az 1. ábrát, amelyen az \(\displaystyle E\) pontból merőlegest állítottunk a \(\displaystyle BC\) befogóra, a merőleges talppontját \(\displaystyle F\)-fel jelöltük.
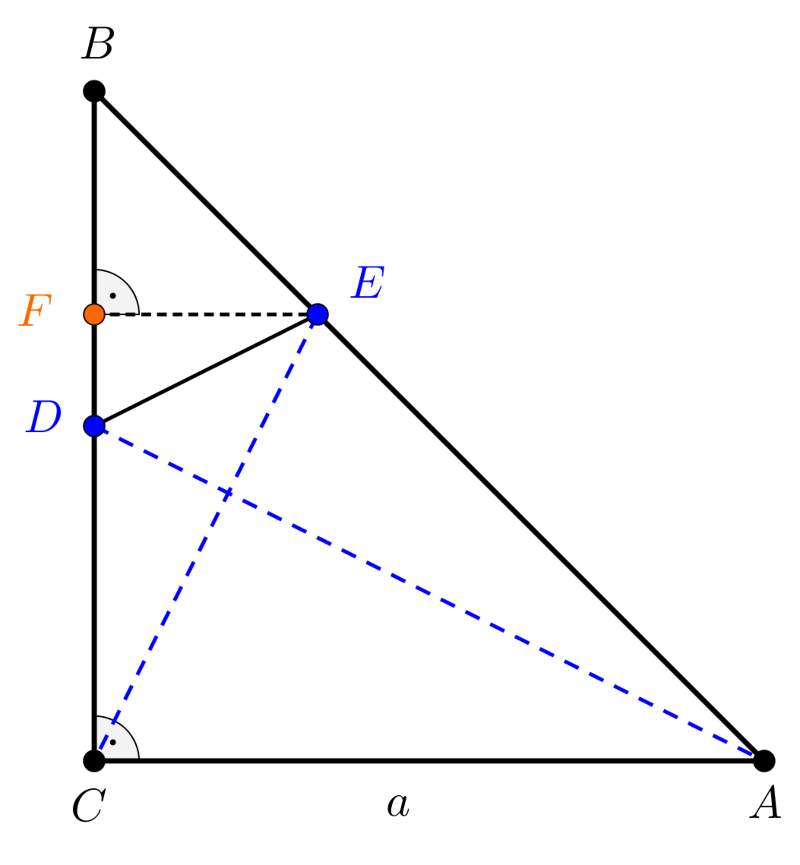
1. ábra
Az \(\displaystyle EF\) szakasz párhuzamos \(\displaystyle AC\)-vel, tehát alkalmazhatjuk a párhuzamos szelőszakaszok tételét:
\(\displaystyle \displaystyle{\frac{BE}{BA}=\frac{EF}{AC}=\frac{EF}{a}},\)
ahonnan \(\displaystyle \displaystyle{\frac{BE}{BA}=\frac{1}{3}}\) miatt \(\displaystyle \displaystyle{}EF=\frac{a}{3}\) következik.
Mivel \(\displaystyle \displaystyle{BD=\frac{a}{2}}\), ezért az \(\displaystyle EBD\) háromszög területe
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{T_{EBD}=\frac{\frac{a}{2}\cdot \frac{a}{3}}{2}=\frac{a^2}{12}}.\) |
Az \(\displaystyle ABC\) háromszög területe \(\displaystyle \displaystyle{T_{ABC}=\frac{a^2}{2}}\), ezért az \(\displaystyle AEDC\) négyszög területe (1) alapján:
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{T_{AEDC}=\frac{a^2}{2}-\frac{a^2}{12}=\frac{5a^2}{12}}.\) |
A Pitagorasz-tétel segítségével kiszámítjuk a \(\displaystyle CEF\) és \(\displaystyle ADC\) derékszögű háromszögek \(\displaystyle CE\) és \(\displaystyle AD\) átfogóinak hosszát:
\(\displaystyle \displaystyle{CE^2=\Bigg(\frac{a}{3}\Bigg)^2+\Bigg(\frac{2a}{3}\Bigg)^2=\frac{5a^2}{9}},\)
és
\(\displaystyle \displaystyle{AD^2=a^2+\Bigg(\frac{a}{2}\Bigg)^2=\frac{5a^2}{4}},\)
ahonnan
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{CE=\frac{a\sqrt{5}}{3};\qquad AD=\frac{a\sqrt{5}}{2}}.\) |
A \(\displaystyle CE\) és \(\displaystyle AD\) szakaszok az \(\displaystyle AEDC\) konvex négyszög átlói, ezért a négyszög területe:
\(\displaystyle \displaystyle{T_{AEDC}=\frac{CE\cdot AD\cdot \sin{\varphi}}{2}},\)
ahol \(\displaystyle \varphi\) a két átló által bezárt szöget jelöli.
A (2) és (3) összefüggések alapján egyszerű számolással kapjuk, hogy
\(\displaystyle \sin{\varphi}=1,\)
ez pedig csak úgy lehetséges, ha \(\displaystyle \varphi=90^{\circ}\). Ezért az \(\displaystyle AD\) és \(\displaystyle CE\) szakaszok valóban merőlegesek egymásra.
2. megoldás. A 2. ábrán a \(\displaystyle C\) pontból az \(\displaystyle A\) és \(\displaystyle B\) pontokba mutató vektorok a következők:
\(\displaystyle \displaystyle{\overrightarrow{CA}=\overrightarrow{a};\qquad \overrightarrow{CB}=\overrightarrow{b}}.\)
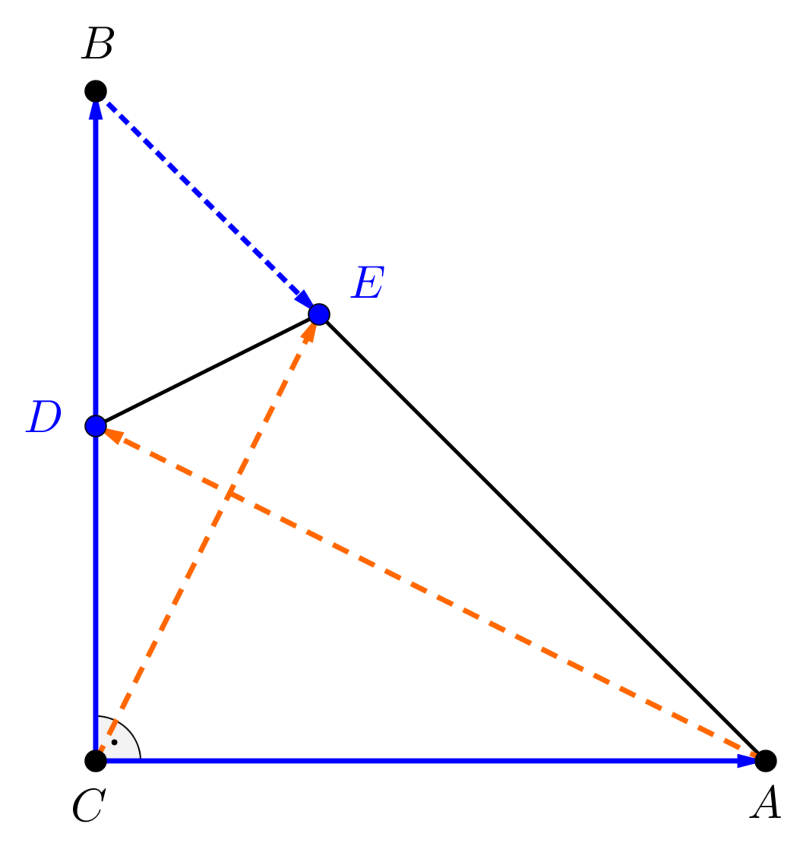
2. ábra
Az \(\displaystyle \overrightarrow{a}\) és \(\displaystyle \overrightarrow{b}\) vektorok hossza nyilván egyenlő, és a két vektor skaláris szorzata zérus, mert a vektorok merőlegesek egymásra.
A vektorok különbségének alapján \(\displaystyle \displaystyle{\overrightarrow{BA}=\overrightarrow{a}-\overrightarrow{b}}\), ugyanakkor \(\displaystyle E\) az \(\displaystyle AB\) szakasz \(\displaystyle B\)-hez közelebbi harmadolópontja, ezért
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{\overrightarrow{BE}=\frac{1}{3}\overrightarrow{BA}=\frac{1}{3}\Big(\overrightarrow{a}-\overrightarrow{b}\Big)}.\) |
Az egymáshoz csatlakoztatott vektorok összegéről tudjuk, hogy \(\displaystyle \displaystyle{\overrightarrow{CE}=\overrightarrow{CB}+\overrightarrow{BE}}\), ezért \(\displaystyle \displaystyle{\overrightarrow{CB}=\overrightarrow{b}}\) és (4) segítségével azt kapjuk, hogy
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{\overrightarrow{CE}=\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}}.\) |
A \(\displaystyle D\) pont felezi a \(\displaystyle CD\) szakaszt, így \(\displaystyle \displaystyle{\overrightarrow{CD}=\frac{1}{2}\overrightarrow{b}}\), ezzel felírhatjuk az \(\displaystyle \displaystyle{\overrightarrow{AD}}\) vektort:
| \(\displaystyle (6)\) | \(\displaystyle \displaystyle{\overrightarrow{AD}=\frac{1}{2}\overrightarrow{b}-\overrightarrow{a}}.\) |
Az (5) és (6) eredmények alapján felírjuk a \(\displaystyle \displaystyle{\overrightarrow{CE}}\) és \(\displaystyle \displaystyle{\overrightarrow{AD}}\) vektorok skaláris szorzatát. Eszerint:
\(\displaystyle \displaystyle{\overrightarrow{CE}\cdot \overrightarrow{AD}=\Bigg(\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}\Bigg)\cdot\Bigg(\frac{1}{2}\overrightarrow{b}-\overrightarrow{a}\Bigg)},\)
ahonnan a műveletek elvégzésével és rendezéssel azt kapjuk, hogy
| \(\displaystyle (7)\) | \(\displaystyle \displaystyle{\overrightarrow{CE}\cdot \overrightarrow{AD}=-\frac{1}{2}\overrightarrow{a}\overrightarrow{b}+\frac{1}{3}{\overrightarrow{b}}^2-\frac{1}{3}{\overrightarrow{a}}^2}.\) |
Mivel az \(\displaystyle \displaystyle{\overrightarrow{a}\cdot \overrightarrow{b}=0}\), továbbá az \(\displaystyle \displaystyle{\overrightarrow{a}}\) és \(\displaystyle \displaystyle{\overrightarrow{b}}\) vektorok négyzete a vektorok hosszának a négyzetével egyenlő, az pedig a két vektor esetében nyilván egyenlő, emiatt a (7) összefüggés jobb oldalának értéke nulla.
A \(\displaystyle \displaystyle{\overrightarrow{CE}}\) és \(\displaystyle \displaystyle{\overrightarrow{AD}}\) vektorok skaláris szorzata tehát zérus, ez akkor és csak akkor lehetséges, ha a két vektor merőleges egymásra. Ezzel igazoltuk a feladat állítását.
3. megoldás. Helyezzük a háromszöget a derékszögű koordináta-rendszerbe úgy, hogy a \(\displaystyle C\) pont legyen az origó, az \(\displaystyle AC\) és \(\displaystyle BC\) szakaszok pedig az \(\displaystyle x\), illetve \(\displaystyle y\) tengelyek pozitív felére essenek. Legyen a háromszög befogóinak hossza \(\displaystyle a\), ezzel az \(\displaystyle A,B\) pontok koordinátái:
| \(\displaystyle (8)\) | \(\displaystyle A\big(a;0\big),\quad B\big(0;a\big).\) |
A \(\displaystyle D\) pont a \(\displaystyle BC\) szakasz felezőpontja, az \(\displaystyle E\) pedig az \(\displaystyle AB\) szakasz \(\displaystyle B\)-hez közelebbi harmadolópontja, ezért a szakaszok osztópontjainak koordinátáira vonatkozó ismeretek és (8) felhasználásával
| \(\displaystyle (9)\) | \(\displaystyle \displaystyle{D\Big(0;\frac{a}{2}\Big);\qquad E\Big(\frac{a}{3};\frac{2a}{3}\Big)}.\) |
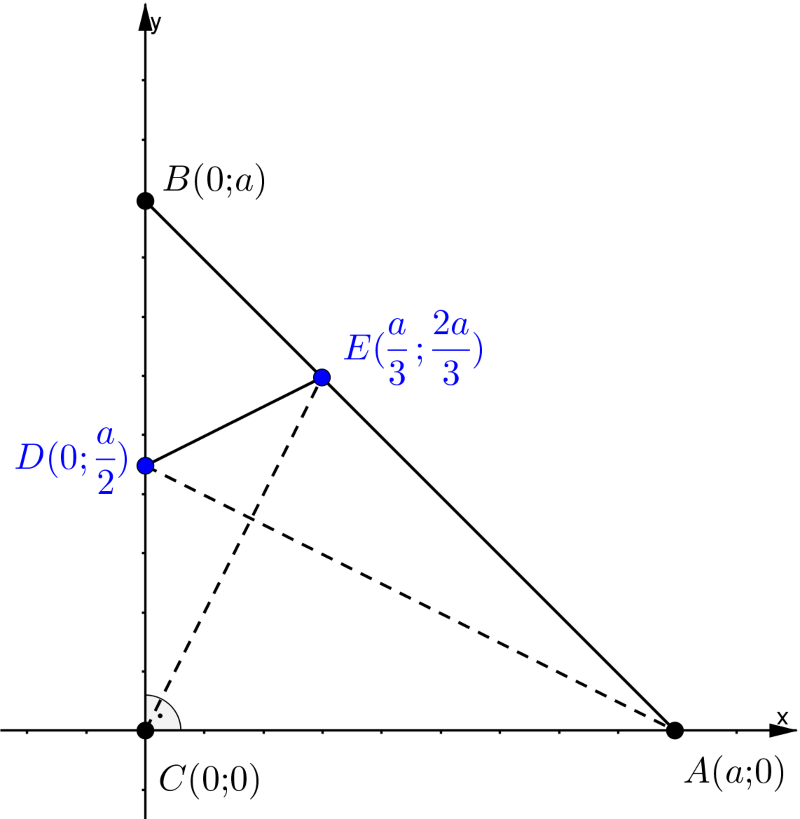
3. ábra
A (9) összefüggés alapján a \(\displaystyle CE\) és \(\displaystyle AD\) egyenesek irányvektora
\(\displaystyle \displaystyle{\overrightarrow{v_{CE}}\Big(\frac{a}{3};\frac{2a}{3}\Big),\qquad \overrightarrow{v_{AD}}\Big(-a;\frac{a}{2}\Big)},\)
tehát a két egyenes meredeksége
| \(\displaystyle (10)\) | \(\displaystyle \displaystyle{m_{CE}=2,\qquad m_{AD}=-\frac{1}{2}}.\) |
A kapott eredmény alapján a két egyenes meredekségének szorzata \(\displaystyle -1\), ez pontosan akkor áll fenn, ha a két egyenes merőleges egymásra, és éppen ezt akartuk bizonyítani.
Statistics:
23 students sent a solution. 5 points: Braun Zsófia, Fiser 234 Boldizsár, Keszthelyi Eszter, Mészáros Anna Veronika, Őzbas Yasin, Richlik Márton, Schneider Dávid, Seprődi Barnabás Bendegúz, Sipeki Márton, Szegedi Ágoston, Szittyai Anna, Waldhauser Miklós. 4 points: Hosszu Noel, Petró Péter, Tomesz László Gergő, Varga Dániel 829, Végh Lilian. 3 points: 1 student. 2 points: 1 student.
Problems in Mathematics of KöMaL, May 2023
