 |
A C. 1771. feladat (2023. május) |
C. 1771. Az \(\displaystyle ABC\) egyenlő szárú derékszögű háromszögben a \(\displaystyle BC\) befogó felezőpontja \(\displaystyle D\), az \(\displaystyle AB\) átfogó \(\displaystyle B\)-hez közelebbi harmadolópontja \(\displaystyle E\). Igazoljuk, hogy \(\displaystyle AD\) és \(\displaystyle CE\) merőlegesek egymásra.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2023. június 12-én LEJÁRT.
1. megoldás. Legyen az \(\displaystyle ABC\) háromszög befogóinak hossza \(\displaystyle a\), ekkor az \(\displaystyle AB\) átfogó hossza \(\displaystyle a\sqrt{2}\). Tekintsük az 1. ábrát, amelyen az \(\displaystyle E\) pontból merőlegest állítottunk a \(\displaystyle BC\) befogóra, a merőleges talppontját \(\displaystyle F\)-fel jelöltük.
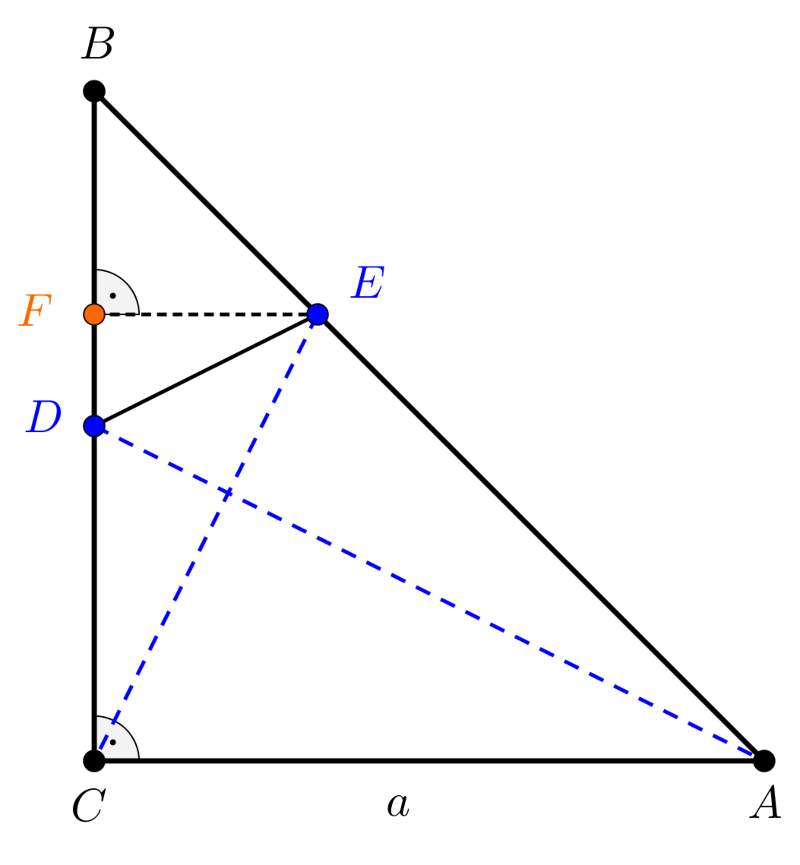
1. ábra
Az \(\displaystyle EF\) szakasz párhuzamos \(\displaystyle AC\)-vel, tehát alkalmazhatjuk a párhuzamos szelőszakaszok tételét:
\(\displaystyle \displaystyle{\frac{BE}{BA}=\frac{EF}{AC}=\frac{EF}{a}},\)
ahonnan \(\displaystyle \displaystyle{\frac{BE}{BA}=\frac{1}{3}}\) miatt \(\displaystyle \displaystyle{}EF=\frac{a}{3}\) következik.
Mivel \(\displaystyle \displaystyle{BD=\frac{a}{2}}\), ezért az \(\displaystyle EBD\) háromszög területe
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{T_{EBD}=\frac{\frac{a}{2}\cdot \frac{a}{3}}{2}=\frac{a^2}{12}}.\) |
Az \(\displaystyle ABC\) háromszög területe \(\displaystyle \displaystyle{T_{ABC}=\frac{a^2}{2}}\), ezért az \(\displaystyle AEDC\) négyszög területe (1) alapján:
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{T_{AEDC}=\frac{a^2}{2}-\frac{a^2}{12}=\frac{5a^2}{12}}.\) |
A Pitagorasz-tétel segítségével kiszámítjuk a \(\displaystyle CEF\) és \(\displaystyle ADC\) derékszögű háromszögek \(\displaystyle CE\) és \(\displaystyle AD\) átfogóinak hosszát:
\(\displaystyle \displaystyle{CE^2=\Bigg(\frac{a}{3}\Bigg)^2+\Bigg(\frac{2a}{3}\Bigg)^2=\frac{5a^2}{9}},\)
és
\(\displaystyle \displaystyle{AD^2=a^2+\Bigg(\frac{a}{2}\Bigg)^2=\frac{5a^2}{4}},\)
ahonnan
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{CE=\frac{a\sqrt{5}}{3};\qquad AD=\frac{a\sqrt{5}}{2}}.\) |
A \(\displaystyle CE\) és \(\displaystyle AD\) szakaszok az \(\displaystyle AEDC\) konvex négyszög átlói, ezért a négyszög területe:
\(\displaystyle \displaystyle{T_{AEDC}=\frac{CE\cdot AD\cdot \sin{\varphi}}{2}},\)
ahol \(\displaystyle \varphi\) a két átló által bezárt szöget jelöli.
A (2) és (3) összefüggések alapján egyszerű számolással kapjuk, hogy
\(\displaystyle \sin{\varphi}=1,\)
ez pedig csak úgy lehetséges, ha \(\displaystyle \varphi=90^{\circ}\). Ezért az \(\displaystyle AD\) és \(\displaystyle CE\) szakaszok valóban merőlegesek egymásra.
2. megoldás. A 2. ábrán a \(\displaystyle C\) pontból az \(\displaystyle A\) és \(\displaystyle B\) pontokba mutató vektorok a következők:
\(\displaystyle \displaystyle{\overrightarrow{CA}=\overrightarrow{a};\qquad \overrightarrow{CB}=\overrightarrow{b}}.\)
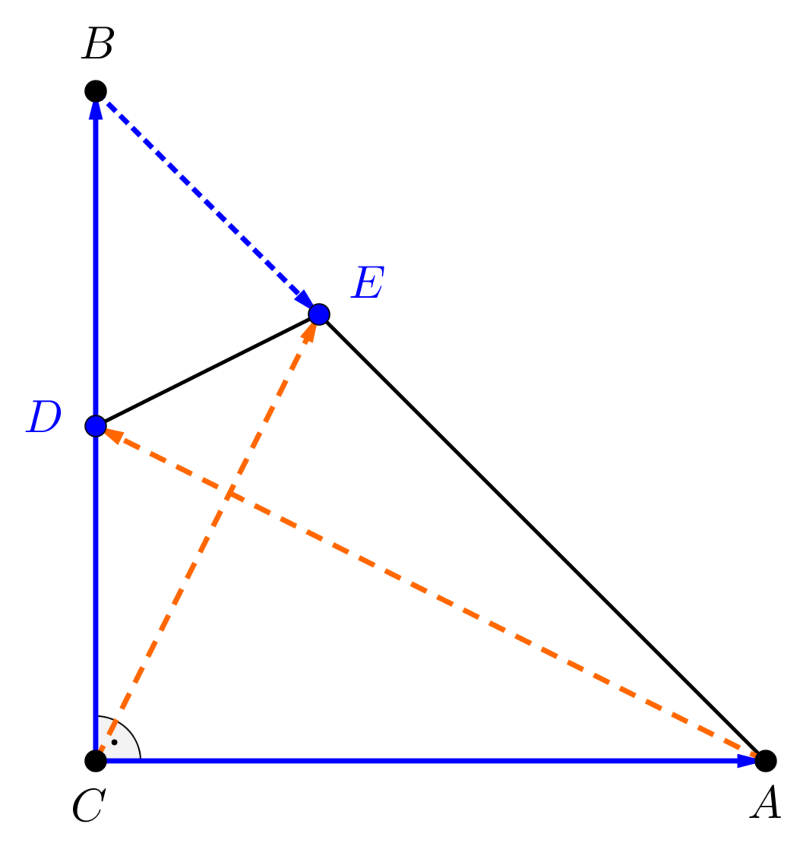
2. ábra
Az \(\displaystyle \overrightarrow{a}\) és \(\displaystyle \overrightarrow{b}\) vektorok hossza nyilván egyenlő, és a két vektor skaláris szorzata zérus, mert a vektorok merőlegesek egymásra.
A vektorok különbségének alapján \(\displaystyle \displaystyle{\overrightarrow{BA}=\overrightarrow{a}-\overrightarrow{b}}\), ugyanakkor \(\displaystyle E\) az \(\displaystyle AB\) szakasz \(\displaystyle B\)-hez közelebbi harmadolópontja, ezért
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{\overrightarrow{BE}=\frac{1}{3}\overrightarrow{BA}=\frac{1}{3}\Big(\overrightarrow{a}-\overrightarrow{b}\Big)}.\) |
Az egymáshoz csatlakoztatott vektorok összegéről tudjuk, hogy \(\displaystyle \displaystyle{\overrightarrow{CE}=\overrightarrow{CB}+\overrightarrow{BE}}\), ezért \(\displaystyle \displaystyle{\overrightarrow{CB}=\overrightarrow{b}}\) és (4) segítségével azt kapjuk, hogy
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{\overrightarrow{CE}=\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}}.\) |
A \(\displaystyle D\) pont felezi a \(\displaystyle CD\) szakaszt, így \(\displaystyle \displaystyle{\overrightarrow{CD}=\frac{1}{2}\overrightarrow{b}}\), ezzel felírhatjuk az \(\displaystyle \displaystyle{\overrightarrow{AD}}\) vektort:
| \(\displaystyle (6)\) | \(\displaystyle \displaystyle{\overrightarrow{AD}=\frac{1}{2}\overrightarrow{b}-\overrightarrow{a}}.\) |
Az (5) és (6) eredmények alapján felírjuk a \(\displaystyle \displaystyle{\overrightarrow{CE}}\) és \(\displaystyle \displaystyle{\overrightarrow{AD}}\) vektorok skaláris szorzatát. Eszerint:
\(\displaystyle \displaystyle{\overrightarrow{CE}\cdot \overrightarrow{AD}=\Bigg(\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}\Bigg)\cdot\Bigg(\frac{1}{2}\overrightarrow{b}-\overrightarrow{a}\Bigg)},\)
ahonnan a műveletek elvégzésével és rendezéssel azt kapjuk, hogy
| \(\displaystyle (7)\) | \(\displaystyle \displaystyle{\overrightarrow{CE}\cdot \overrightarrow{AD}=-\frac{1}{2}\overrightarrow{a}\overrightarrow{b}+\frac{1}{3}{\overrightarrow{b}}^2-\frac{1}{3}{\overrightarrow{a}}^2}.\) |
Mivel az \(\displaystyle \displaystyle{\overrightarrow{a}\cdot \overrightarrow{b}=0}\), továbbá az \(\displaystyle \displaystyle{\overrightarrow{a}}\) és \(\displaystyle \displaystyle{\overrightarrow{b}}\) vektorok négyzete a vektorok hosszának a négyzetével egyenlő, az pedig a két vektor esetében nyilván egyenlő, emiatt a (7) összefüggés jobb oldalának értéke nulla.
A \(\displaystyle \displaystyle{\overrightarrow{CE}}\) és \(\displaystyle \displaystyle{\overrightarrow{AD}}\) vektorok skaláris szorzata tehát zérus, ez akkor és csak akkor lehetséges, ha a két vektor merőleges egymásra. Ezzel igazoltuk a feladat állítását.
3. megoldás. Helyezzük a háromszöget a derékszögű koordináta-rendszerbe úgy, hogy a \(\displaystyle C\) pont legyen az origó, az \(\displaystyle AC\) és \(\displaystyle BC\) szakaszok pedig az \(\displaystyle x\), illetve \(\displaystyle y\) tengelyek pozitív felére essenek. Legyen a háromszög befogóinak hossza \(\displaystyle a\), ezzel az \(\displaystyle A,B\) pontok koordinátái:
| \(\displaystyle (8)\) | \(\displaystyle A\big(a;0\big),\quad B\big(0;a\big).\) |
A \(\displaystyle D\) pont a \(\displaystyle BC\) szakasz felezőpontja, az \(\displaystyle E\) pedig az \(\displaystyle AB\) szakasz \(\displaystyle B\)-hez közelebbi harmadolópontja, ezért a szakaszok osztópontjainak koordinátáira vonatkozó ismeretek és (8) felhasználásával
| \(\displaystyle (9)\) | \(\displaystyle \displaystyle{D\Big(0;\frac{a}{2}\Big);\qquad E\Big(\frac{a}{3};\frac{2a}{3}\Big)}.\) |
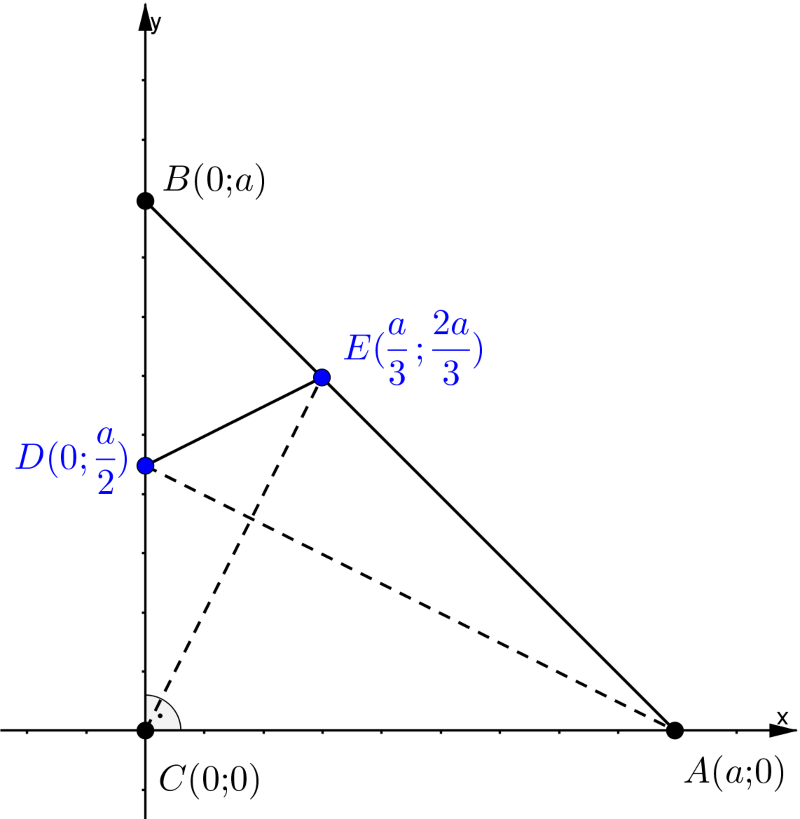
3. ábra
A (9) összefüggés alapján a \(\displaystyle CE\) és \(\displaystyle AD\) egyenesek irányvektora
\(\displaystyle \displaystyle{\overrightarrow{v_{CE}}\Big(\frac{a}{3};\frac{2a}{3}\Big),\qquad \overrightarrow{v_{AD}}\Big(-a;\frac{a}{2}\Big)},\)
tehát a két egyenes meredeksége
| \(\displaystyle (10)\) | \(\displaystyle \displaystyle{m_{CE}=2,\qquad m_{AD}=-\frac{1}{2}}.\) |
A kapott eredmény alapján a két egyenes meredekségének szorzata \(\displaystyle -1\), ez pontosan akkor áll fenn, ha a két egyenes merőleges egymásra, és éppen ezt akartuk bizonyítani.
Statisztika:
23 dolgozat érkezett. 5 pontot kapott: Braun Zsófia, Fiser 234 Boldizsár, Keszthelyi Eszter, Mészáros Anna Veronika, Őzbas Yasin, Richlik Márton, Schneider Dávid, Seprődi Barnabás Bendegúz, Sipeki Márton, Szegedi Ágoston, Szittyai Anna, Waldhauser Miklós. 4 pontot kapott: Hosszu Noel, Petró Péter, Tomesz László Gergő, Varga Dániel 829, Végh Lilian. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2023. májusi matematika feladatai
