A C. 1784. feladat (2023. november)

C. 1784. Az \(\displaystyle ABC\) derékszögű háromszög rövidebbik befogója egységnyi hosszúságú. A derékszögű csúcsból az \(\displaystyle AB\) átfogóra bocsátott magasság a hegyesszögek szögfelezőivel olyan \(\displaystyle \varphi\) és \(\displaystyle \varepsilon\) szögeket zár be, amelyekre

\(\displaystyle \frac{\varphi}{\varepsilon}=\frac{4}{5}. \)

Határozzuk meg a háromszög szögeit és az átfogóhoz tartozó magasság hosszát.

Javasolta: Bíró Bálint (Eger)

(5 pont)

A beküldési határidő 2023. december 11-én LEJÁRT.

Megoldás.

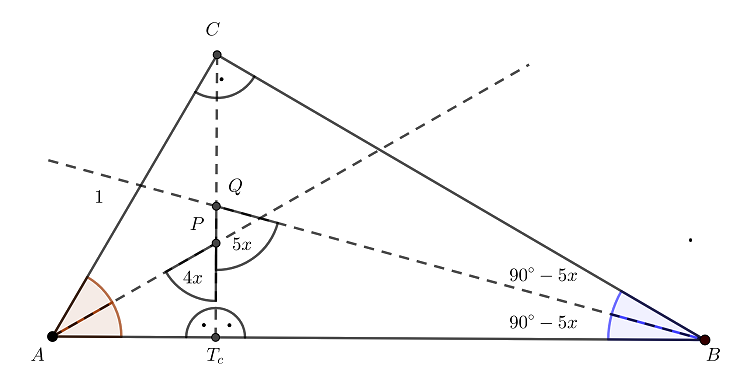
Az ábrán látható \(\displaystyle ABC\) háromszög teljesíti a feladat feltételeit: derékszögű, és rövidebbik befogója \(\displaystyle 1\).

Tekintve, hogy \(\displaystyle AC< CB\), az is igaz, hogy \(\displaystyle CAB\sphericalangle >CBA\sphericalangle\), hiszen nagyobb oldallal szemközt nagyobb szög található. Az utóbbi egyenlőtlenségből viszont az következik, hogy az \(\displaystyle APT_c\) és \(\displaystyle BQT_c\) derékszögű háromszögek hegyesszögeire az alábbi összefüggések igazak (ahol \(\displaystyle AP\) és \(\displaystyle BQ\) a feladat szövegében szereplő szögfelezők):

\(\displaystyle PAT_c \sphericalangle=\frac{CAB\sphericalangle}{2} > \frac{CBA\sphericalangle}{2}=QBT_c \sphericalangle.\)

A háromszög belső szögeinek összege \(\displaystyle 180^{\circ}\), tehát az is teljesül, hogy

\(\displaystyle \displaystyle{APT_c \sphericalangle < BQT_c\sphericalangle}.\)

Tekintve a feladat szövegében megadott feltételt erre az utóbbi két szögre, azt kapjuk, hogy

\(\displaystyle \displaystyle{\varphi=APT_c \sphericalangle=4x},\)

\(\displaystyle \displaystyle{\epsilon=BQT_c\sphericalangle=5x},\)

ahogyan ezt az ábrán is jelöltük. Mindezek alapján

\(\displaystyle CAT_c\sphericalangle=2\cdot(90^{\circ}-4x),\qquad CBT_c\sphericalangle=2\cdot(90^{\circ}-5x).\)

Ebből az \(\displaystyle ABC\) háromszög hegyesszögeire az alábbi egyenlet adódik:

\(\displaystyle 180^{\circ}-8x+180^{\circ}-10x=90^{\circ},\)

az egyenlet megoldása \(\displaystyle x=15^{\circ}\). Az \(\displaystyle ABC\) háromszög hegyesszögei tehát

\(\displaystyle CAT_c=CAB\sphericalangle=180^{\circ}-8\cdot15^{\circ}=60^{\circ},\)

\(\displaystyle CBT_c=ABC\sphericalangle=180^{\circ}-10\cdot15^{\circ}=30^{\circ}.\)

Ebből következik, hogy az \(\displaystyle ACT_c\) háromszög egy szabályos háromszög fele, így \(\displaystyle \displaystyle{AT_c=\frac{1}{2}}\). Ha erre a háromszögre alkalmazzuk a Pitagorasz-tételt, akkor azt kapjuk, hogy az \(\displaystyle ABC\) derékszögű háromszög \(\displaystyle AB\) átfogójához tartozó magassága:

\(\displaystyle \displaystyle{CT_c=\frac{\sqrt{3}}{2}}.\)

Statisztika:

220 dolgozat érkezett.
5 pontot kapott:	58 versenyző.
4 pontot kapott:	101 versenyző.
3 pontot kapott:	14 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	6 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	19 dolgozat.

A KöMaL 2023. novemberi matematika feladatai