 |
A C. 1804. feladat (2024. március) |
C. 1804. Az \(\displaystyle ABC\) háromszög \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) oldalainak felezőpontja rendre \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\). Az \(\displaystyle AFE\), \(\displaystyle BDF\), \(\displaystyle CED\) háromszögek beírt köreinek középpontja rendre \(\displaystyle K_a\), \(\displaystyle K_b\), \(\displaystyle K_c\). Bizonyítsuk be, hogy a \(\displaystyle K_aFDE\), \(\displaystyle K_bDEF\) és \(\displaystyle K_cEFD\) négyszögek területének összege az \(\displaystyle ABC\) háromszög területével egyenlő.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2024. április 10-én LEJÁRT.
Megoldás.
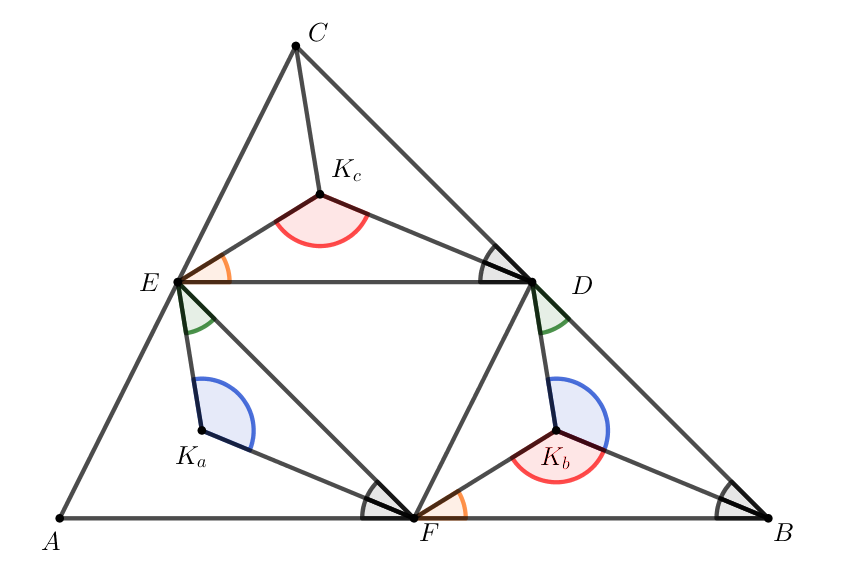
Az \(\displaystyle ABC\) háromszög középvonalai az \(\displaystyle EF\), \(\displaystyle FD\) és \(\displaystyle DE\) szakaszok. Ebből következik, hogy \(\displaystyle EF\parallel CB\), \(\displaystyle FD\parallel AC\), \(\displaystyle DE\parallel BA\), és \(\displaystyle \displaystyle{EF=\frac{1}{2}CB}\), \(\displaystyle \displaystyle{FD=\frac{1}{2}AC}\), \(\displaystyle \displaystyle{DE=\frac{1}{2}BA}\). A megfelelő szögek páronkénti egyenlőségéből és a megfelelő szakaszok hosszából következik, hogy \(\displaystyle ABC \triangle \sim AFE \triangle\), valamint \(\displaystyle AFE\triangle \cong FBD \triangle \cong EDC \triangle \cong DEF \triangle\), továbbá az is igaz, hogy
| \(\displaystyle (1)\) | \(\displaystyle \frac{T_{DEF}}{T_{ABC}}=\Bigg(\frac{1}{2}\Bigg)^2=\frac{1}{4}.\) |
A feladatban szereplő területösszeget jelöljük \(\displaystyle S\)-sel:
\(\displaystyle S=T_{K_aFDE}+T_{K_bDEF}+T_{K_cEFD}.\)
Mindhárom négyszöget két-két háromszögre vághatunk, így a területösszegekre igaz, hogy:
| \(\displaystyle (2)\) | \(\displaystyle T_{K_aFDE}=T_{DEF}+T_{EK_aF}, \) |
| \(\displaystyle (3)\) | \(\displaystyle T_{K_bDEF}=T_{DEF}+T_{DFK_b}, \) |
| \(\displaystyle (4)\) | \(\displaystyle T_{K_cEFD}=T_{DEF}+T_{K_cED}. \) |
Ha ezeket összeadjuk, azt kapjuk, hogy \(\displaystyle (2)+(3)+(4)\):
| \(\displaystyle (5)\) | \(\displaystyle S=3\cdot T_{DEF} + T_{EK_aF} + T_{DFK_b} + T_{K_cED}. \) |
Tudjuk, hogy az \(\displaystyle AFE\triangle \cong FBD \triangle\), és a beírt kör középpontja a belső szögfelezők metszéspontja, ezért \(\displaystyle EK_a \parallel DK_b\), \(\displaystyle K_aF \parallel K_bB\), továbbá \(\displaystyle EF \parallel DB\) és \(\displaystyle EF=DB\), ezért az alábbi egybevágóság teljesül:
\(\displaystyle EK_aF \triangle \cong DK_bB\triangle, \)
és ugyanígy igaz, hogy
\(\displaystyle K_cED \triangle \cong K_bFB \triangle,\hspace{0.3cm}\text{tehát} \)
\(\displaystyle T_{EK_aF} + T_{DFK_b} + T_{K_cED} = T_{DK_bB} + T_{DFK_b} + T_{K_bFB} = T_{FBD}=T_{DEF}. \)
Ebből, az (5)-ből és az (1)-ből következik, hogy
\(\displaystyle S=4\cdot T_{DEF}=T_{ABC}.\)
Statisztika:
154 dolgozat érkezett. 5 pontot kapott: 84 versenyző. 4 pontot kapott: 26 versenyző. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 4 versenyző. Nem versenyszerű: 9 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 10 dolgozat.
A KöMaL 2024. márciusi matematika feladatai

