A C. 868. feladat (2006. október)

C. 868. Adott a síkban négy különböző pont. A négy pont közötti hat távolság közül négy távolság egységnyi, egy pedig 1,2. Mekkora lehet az ismeretlen hatodik távolság?

(5 pont)

A beküldési határidő 2006. november 15-én LEJÁRT.

Megoldás. Ha a négy egységnyi távolság közül három egy szabályos háromszöget határoz meg, akkor (ezt a három csúcsot A-val, B-vel és C-vel jelölve) két lehetőség van a többi szakasz elhelyezkedésére.

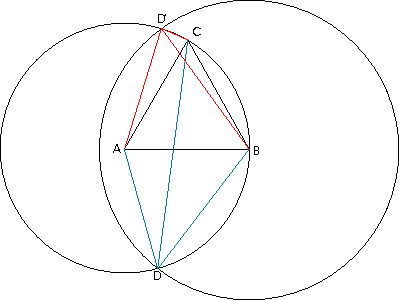
Mindkét esetben az 1,2 hosszú és az egységnyi oldal háromszöget alkot ABC egyik (mondjuk AB) oldalával. Ennek 3. csúcsát D-vel, illetve D'-vel jelölve az ABD (illetve ABD') háromszög oldalaiból kiszámítható koszinusz-tétellel az ABD=ABD', értéke 53,13^o-nak adódik. Ezután a CBD, illetve CBD' háromszögben az ismeretlen CD, illetve CD' oldal szintén a koszinusz tétellel kapható meg, hosszára 1,84, illetve 0,24 adódik.

Ha a négy egységnyi hosszú oldal egy rombuszt alkot, akkor annak átlói 1,2, illetve az ismeretlen x. A Pitagorasz tételből 1²=(1,2/2)²+(x/2)², innen x=1,6.

Tehát az ismeretlen hatodik távolság 0,24, 1,6 vagy 1,84 lehet.

Statisztika:

438 dolgozat érkezett.
5 pontot kapott:	80 versenyző.
4 pontot kapott:	69 versenyző.
3 pontot kapott:	97 versenyző.
2 pontot kapott:	130 versenyző.
1 pontot kapott:	21 versenyző.
0 pontot kapott:	35 versenyző.
Nem versenyszerű:	6 dolgozat.

A KöMaL 2006. októberi matematika feladatai