A C. 935. feladat (2008. március)

C. 935. Feldarabolható-e egy szabályos háromszög

a) 2007,

b) 2008 darab szabályos háromszögre?

(5 pont)

A beküldési határidő 2008. április 15-én LEJÁRT.

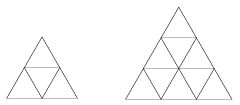
Megoldás: b) Az ábra mutatja, hogy a középvonalak berajzolásával egy tetszőleges szabályos háromszöget négy egybevágó szabályos háromszögre fel lehet bontani. A háromszögek számát így lehet 3-mal lehet növelni. Mivel 1 háromszögből indulunk el, és 2008=1+669^.3, azért ha 669-szer elismételjük a felosztást, akkor a végén 2008 háromszög lesz. (Minden lépésben kiválasztjuk valamelyik még nem tovább osztott szabályos háromszöget.)

b) A másik ábra azt mutatja, hogy két-két szomszédos oldal megfelelő harmadolópontjait összekötve a keletkezett párhuzamosokkal 9 egybevágó háromszögre lehet felbontani egy szabályos háromszöget. Mivel 2007=9+666^.3, ezért ezt a kilenc háromszöget a b) részben látott módon 666 lépésben tovább osztva 2007 háromszöget kapunk.

Statisztika:

237 dolgozat érkezett.
5 pontot kapott:	136 versenyző.
4 pontot kapott:	9 versenyző.
2 pontot kapott:	53 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	20 versenyző.
Nem versenyszerű:	8 dolgozat.

A KöMaL 2008. márciusi matematika feladatai