A C. 953. feladat (2008. szeptember)

C. 953. Egy derékszögű trapézba kör írható. Igazoljuk, hogy a derékszögű szár hossza harmonikus közepe az alapok hosszának.

(5 pont)

A beküldési határidő 2008. október 15-én LEJÁRT.

Megoldás. A kör középpontját jelölje O, az O-ból a trapéz nem derékszögű szárára állított merőleges talppontját T, az alapokra emelt merőlegesek talppontját pedig R, illetve S.

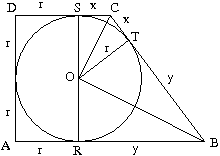
DC a kör érintője, így merőleges SO-ra. Ugyanígy AB merőleges RO-ra. Mivel $DC\parallel AB$ , ezért az O-ból rájuk állított merőlegesek egy egyenesbe esnek: S, O és R egy egyenesen vannak. Az ARSD négyszög téglalap, hiszen szomszédos oldalai merőlegesek egymásra. Ezért AD=RS=2r. Mivel egy pontból a körhöz húzott érintési szakaszok hossza egyenlő, ezért az ábrán látható szakaszok keletkeznek, hosszukat jelölje r (ami egyenlő a beírt kör sugarával), illetve x és y.

COB $\angle$ =180^o-(DCB $\angle$ /2+ABC $\angle$ /2)=180^o-90^o=90^o. A COB háromszögre alkalmazva a magasságtételt kapjuk, hogy r²=xy.

Az alapok hosszának harmonikus közepét felírva, majd átalakítva:

$\frac{2}{\frac{1}{r+x}+\frac{1}{r+y}}=$

$=\frac{2(r+x)(r+y)}{r+y+r+x}=\frac{2(r^2+r(x+y)+xy)}{2r+(x+y)}=$

$=\frac{2(r^2+r(x+y)+r^2)}{2r+(x+y)}=\frac{4r^2+2r(x+y)}{2r+(x+y)}=2r,$

ami épp a derékszögű szár hossza.

Statisztika:

382 dolgozat érkezett.

5 pontot kapott: 236 versenyző.

4 pontot kapott: 64 versenyző.

3 pontot kapott: 9 versenyző.

2 pontot kapott: 13 versenyző.

1 pontot kapott: 12 versenyző.

0 pontot kapott: 41 versenyző.

Nem versenyszerű: 7 dolgozat.

A KöMaL 2008. szeptemberi matematika feladatai

382 dolgozat érkezett.
5 pontot kapott:	236 versenyző.
4 pontot kapott:	64 versenyző.
3 pontot kapott:	9 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	12 versenyző.
0 pontot kapott:	41 versenyző.
Nem versenyszerű:	7 dolgozat.

Már regisztráltál?
Új vendég vagy?