A C. 998. feladat (2009. szeptember)

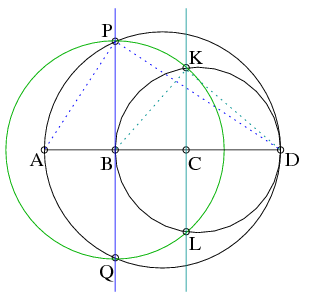
C. 998. Az A, B, C és D pontok ebben a sorrendben egy egyenesre illeszkednek, és AB=BC. Állítsunk B-ben és C-ben az AD-re merőlegest. A B-ben állított merőleges az AD átmérőjű kört P-ben és Q-ban, a C-ben állított merőleges a BD átmérőjű kört a K és L pontokban metszi. Igazoljuk, hogy a P, K, L és Q pontokra illeszkedő kör középpontja B.

(5 pont)

A beküldési határidő 2009. október 12-én LEJÁRT.

Megoldás. A feladatbeli egyenesek, körök, metszéspontok mind szimmetrikusak az $\displaystyle AD$ egyenesre (mert $\displaystyle PQ$ és $\displaystyle KL$ egyenese merőleges $\displaystyle AD$-re, a köröknek pedig centrálisa.) Legyenek $\displaystyle AB=BC=a$ és $\displaystyle CD=b$ a szakaszok hosszai. Így $\displaystyle AD=2a+b$ és $\displaystyle BD=a+b$ az átmérők. Az $\displaystyle APD$ háromszög és a $\displaystyle BKD$ háromszög derékszögű (Thálesz-tétel). Az $\displaystyle APB$ háromszögben $\displaystyle PB$ magasság a feladat szerint, és a magasság-tételt felírva $\displaystyle PB=\sqrt{AB \cdot BD}=\sqrt{a(a+b)}$. $\displaystyle BKD$ háromszögben a befogótételt használva $\displaystyle BK=\sqrt{BC \cdot CD}=\sqrt{a(a+b)}$. Tehát $\displaystyle BP=BK$ és a szimmetria miatt $\displaystyle BP=BL=BQ$, azaz $\displaystyle P$, $\displaystyle K$, $\displaystyle L$, $\displaystyle Q$ pontok mind ugyanakkora távolságra vannak $\displaystyle B$-től, azaz a $\displaystyle B$ középpontú $\displaystyle \sqrt{a(a+b)}$ sugarú körben $\displaystyle PKLQ$ húrnégyszög.

Statisztika:

292 dolgozat érkezett.
5 pontot kapott:	152 versenyző.
4 pontot kapott:	58 versenyző.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	14 versenyző.
0 pontot kapott:	58 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2009. szeptemberi matematika feladatai