A G. 634. feladat (2018. április)

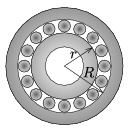
G. 634. Az ábrán látható golyóscsapágy belső gyűrűje mozdulatlan, a golyók középpontjai 0,2 m/s sebességgel futnak körbe. Mekkora a külső gyűrű fordulatszáma, ha \(\displaystyle r=3\) cm, \(\displaystyle R=4\) cm?

(3 pont)

A beküldési határidő 2018. május 10-én LEJÁRT.

Megoldás. Ha a golyók sem a külső, sem pedig a belső gyűrűn nem csúsznak (hanem csak gördülnek), akkor a külső gyűrű belső oldalának sebessége éppen kétszer nagyobb, mint a golyók középpontjának sebessége, vagyis 0,4 m/s nagyságú. Ekkora sebességgel egy teljes fordulatot, azaz \(\displaystyle 2R\pi\approx0{,}25\) m utat

\(\displaystyle T=\frac{0{,}25~\rm m}{0{,}4~\rm m/s}=0{,}63~\rm s\)

idő alatt teszi meg a külső gyűrű. Ez

\(\displaystyle f=\frac{1}{T}\approx 1{,}6~\frac{1}{\rm s}\approx 96~\frac{1}{\rm perc}\)

fordulatszámnak felel meg.

Statisztika:

41 dolgozat érkezett.
3 pontot kapott:	Antal Virág Anna, Bárdos Deák Botond, Barta Gergely, Bekes Barnabás, Forgács Kata, Kis-Bogdán Kolos, Láng Erik, Menyhárt Tamás, Nagy Zalán, Papanitz Ákos, Papp Marcell Miklós, Toronyi András.
2 pontot kapott:	Kovács Kristóf, Németh Ábel, Szeibel Richard.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	21 versenyző.

A KöMaL 2018. áprilisi fizika feladatai