A G. 650. feladat (2018. november)

G. 650. Áron azzal szórakozott, hogy a 30 cm hosszú, egyenes vonalzója végére tette a kicsi radírját, és az asztal szélére merőlegesen csúsztatta kifelé a vonalzót. Megmérte, hogy ha 11 cm-nél jobban kitolja, akkor a vonalzó lebillen. Mekkora a vonalzó és a radír tömegének aránya?

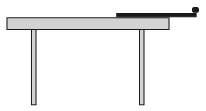
(3 pont)

A beküldési határidő 2018. december 10-én LEJÁRT.

Megoldás. Legyen a vonalzó tömege \(\displaystyle M\), a radír tömege pedig \(\displaystyle m\). A lebillenés határhelyzetében a vonalzó középpontja 4 cm-re, a radír pedig 11 cm-re van az asztal szélétől. A forgatónyomatékok egyensúlyából következik, hogy \(\displaystyle 11\,m=4\,M\), vagyis a keresett tömegarány:

\(\displaystyle \frac{M}{m}=\frac{11}{4}=2{,}75.\)

Statisztika:

91 dolgozat érkezett.
3 pontot kapott:	Arhaan Ahmad, Bányai Kristóf, Barátfalvi László Imre, Bodzsár Míra, Csapó Tamás, Egri Mátyás, Egyed Márton, Farkas 200 Eszter, Ferjancsik Zaránd, Fincur Ádám, Forgó Réka, Geraszin Nikolett, Győrffy Attila, Hamar János, Heizer Koppány, Hruby Lili, Juhász Márk Hunor, Kalmár Levente, Kinyó Kincső, Kis 128 Ágnes , Kis-Bogdán Kolos, Koleszár Benedek, Kovács Alex, Kovács Móric, Láng Erik, Lovas Márton, Markó Péter , Mészáros Emma, Nagy Zalán, Nagyváradi Dániel, Papp Marcell Miklós, Patricia Janecsko, Sárvári Borka Luca, Sebestyén József Tas, Sebestyén Pál Botond, Seres-Szabó Márton, Somlán Gellért, Stein Felix, Števko Daniel, Szántó Barnabás, Szőllősi Gergely, Tallósy Péter, Téglás Panna, Thierry Armand, Török 111 László, Török 517 Mihály, Tüske Milán, Virág Levente, Williams Hajna, Zsigmond Botond.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	32 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2018. novemberi fizika feladatai