 |
A G. 660. feladat (2019. január) |
G. 660. Egy falhoz kötött, vízszintesen kifeszített, rugalmas szalagon egy csiga mászik 1 m/h sebességgel. A csiga a faltól indul, a szalag kezdeti hossza 2 m. Az indulástól számított minden óra végén a szalagot a végénél fogva 1 méterrel megnyújtjuk. Az indulás után mennyi idővel érkezik a csiga a szalag végére?
(4 pont)
A beküldési határidő 2019. február 11-én LEJÁRT.
Megoldás. A csiga, illetve a szalag végének távolsága a faltól az alábbiak szerint változik:
1. állapot: Közvetlenül az első óra eltelte előtt a szalag hossza 2 m, a csiga a faltól 1 méterre, a szalag \(\displaystyle \tfrac12\) részénél lesz.
2. állapot: Közvetlenül az első óra eltelte után a szalag hossza 3 méter, és a csiga a szalag \(\displaystyle \tfrac12\) részénél van, tehát a faltól 1,5 méternyire kerül.
3. állapot: Közvetlenül a második óra eltelte előtt a csiga a faltól 2,5 méterre van, ez a szalag hosszának \(\displaystyle \tfrac56\) részének felel meg.
4. állapot: Közvetlenül a második óra eltelte után a szalag hossza 4 méterre nő, a csiga pedig ennek \(\displaystyle \tfrac56\) részénél, a faltól \(\displaystyle \tfrac{10}3\) méterre lesz.
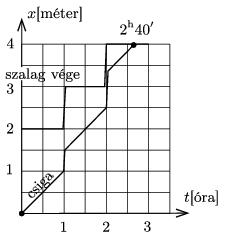
5. állapot: A csiga \(\displaystyle 4-\tfrac{10}3=\tfrac23\) méternyi utat \(\displaystyle \tfrac23\) óra, vagyis 40 perc alatt tesz meg, tehát az indulástól számítva \(\displaystyle 2^{\rm h}40'\) alatt érkezik a szalag végéhez. A csiga helyzetét és a szalag végének helyét az idő függvényében az alábbi ábra mutatja.
Statisztika:
71 dolgozat érkezett. 4 pontot kapott: 57 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2019. januári fizika feladatai

