Problem G. 662. (February 2019)

G. 662. A disc with greater radius and two smaller cylinder are attached to each other concentrically; the assembly is shown in figures \(\displaystyle (a)\) and \(\displaystyle (b)\). Two pieces of cords were wrapped around the cylinders, and their ends are moved horizontally at constant speed of \(\displaystyle v\), with the help of a rod.

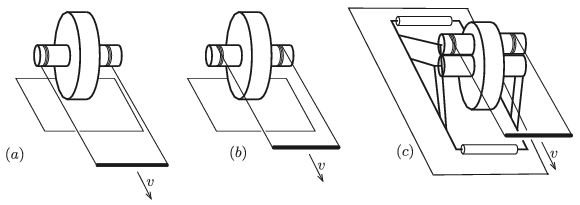
In the \(\displaystyle (c)\) case, there is another cylinder, which can rotate freely, above the cylinder on the original device. The cylinders have the same radius, and touch each other tightly. A rod structure is attached to the cylinders in order to prevent them from falling. A piece of cord is wrapped around the top cylinder and the end is again pulled at a constant speed of \(\displaystyle v\). The discs do not slip on the ground and the cylinders do not slip on each other.

In what direction will the centre of the disc move in each case? Will the speed of the centre of the disc be greater or smaller than \(\displaystyle v\) in each case?

(3 pont)

Deadline expired on March 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Mindhárom esetben a korong középpontja ugyanolyan irányban (előrefelé) mozog, mint amerre a fonalakat húzzuk. Az \(\displaystyle (a)\) és a \(\displaystyle (c)\) esetben a korong \(\displaystyle v\)-nél nagyobb sebességgel, a \(\displaystyle (b)\) esetben pedig \(\displaystyle v\)-nél kisebb sebességgel gördül előre a korong.

Megjegyzés. Ha a korong sugara \(\displaystyle R\), a kis hengereké pedig \(\displaystyle r\), akkor a korong középpontjának sebessége a három esetben:

\(\displaystyle u_a=u_c=\frac{R}{R-r}v,\qquad u_b=\frac{R}{R+r}v.\)

Ezeket az összefüggéseket (amelyek levezetése nem tartozik a feladathoz) legkönnyebben a korong középpontjával együtt mozgó koordináta-rendszerben lehet megkapni. Ebből a rendszerből nézve a korong középpontja áll (tehát a korong csak forog), a fonál \(\displaystyle v-u\) sebességgel halad előrefelé, a talaj pedig \(\displaystyle u\) sebességgel hátrafelé. Ezek a sebességek a rögzítettnek tekinthető forgástengelytől mért távolsággal arányosak:

\(\displaystyle \frac{v-u_a}{u_a}=-\frac{r}{R};\qquad \frac{v-u_b}{u_b}=+\frac{r}{R};\qquad \frac{ u_c-v}{u_c}=+\frac{r}{R}.\)

Statistics:

27 students sent a solution.
3 points:	Sárvári Borka Luca.
2 points:	Bánáti Tamás, Koczkás József Dániel, Kovács Alex, Markó Péter , Sebestyén József Tas, Somlán Gellért, Szántó Barnabás, Szőllősi Gergely, Téglás Panna, Török 111 László.
1 point:	6 students.
0 point:	10 students.

Problems in Physics of KöMaL, February 2019