 |
A G. 666. feladat (2019. március) |
G. 666. Az ábrán egy vidámparki szórakoztatószerkezet vázlata látható. A középső, nagy henger egyenletesen forog körbe. A rajta lévő négy rögzítőkar segítségével négy tengelyezett, kör alakú ,,gondola'' is körbejár. Minden gondola közepéhez egy-egy korongot rögzítettek, melyek ugyanúgy vannak tengelyezve, mint a gondola. A gondolák közepén lévő korongok csúszásmentes szíjáttétel segítségével csatlakoznak a szerkezet közepén található \(\displaystyle K\) koronghoz, ami rögzített, tehát egyáltalán nem forog. (Az ábrán – az áttekinthetőség kedvéért – csak az egyik gondolánál tüntettük fel ezt a szíjat.)
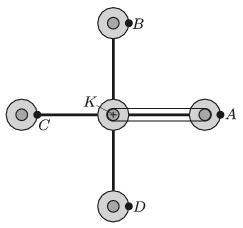
Az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontok egy-egy utast ábrázolnak. Milyen pályán mozognak az utasok? Hogyan változik a közöttük lévő távolság a forgás közben? (A szerkezet vízszintes síkban forog, a tengelyek mind függőlegesek.)
Amerikai feladat nyomán
(4 pont)
A beküldési határidő 2019. április 10-én LEJÁRT.
Megoldás. Az elforduló gondolák – a szíjáttétek miatt – ugyanakkora szöggel, de ellenkező irányban fordulnak el a rögzítőkarokhoz képest, mint amekkora a karok elfordulása a talajhoz viszonyítva. (Az \(\displaystyle A\) jelű utas például az \(\displaystyle A'\) helyre kerül.) Az egyes utasok pályája egy olyan kör lesz, amely a gondolák középpontjai által végigjárt körhöz képest bizonyos távolsággal eltolódott. Az utasok egymástól mért távolsága a mozgás során nem változik. Mindez csak akkor érvényes, ha az utasok a gondolák középpontjához képest ugyanakkora távolságban és ugyanabban az irányban eltolva helyezkednek el.
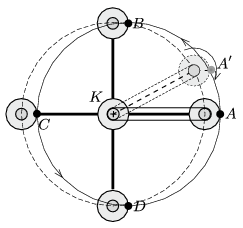
Az utasok mozgását leírhatjuk a gondolákkal együtt forgó koordináta-rendszerből is. Innen nézve az utasok mozdulatlan középpontú körök mentén egyenletes körmozgást végeznek, és a távolságuk – mint a jól beállított faliórák nagymutató végpontjainak távolsága – időben állandó marad.
Statisztika:
38 dolgozat érkezett. 4 pontot kapott: Bányai Kristóf, Csapó Tamás, Kis-Bogdán Kolos, Koczkás József Dániel, Kovács Alex, Markó Péter , Nagy Zalán, Papp Marcell Miklós, Sebestyén József Tas, Somlán Gellért, Szántó Barnabás, Szeibel Richard, Szőllősi Gergely. 3 pontot kapott: Buránszki Domonkos, Heizer Koppány, Juhász Márk Hunor. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 8 versenyző. 0 pontot kapott: 6 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2019. márciusi fizika feladatai

