A G. 695. feladat (2020. január)

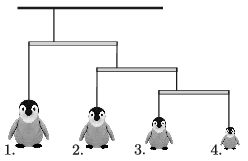
G. 695. Játékpingvineket függesztettek egy mozgó szobadíszre. A nagyon könnyű rudakat a negyedelőpontjukban függesztették fel, és így egyensúlyban vannak. Mekkora a 2., a 3. és a 4. pingvin tömege, ha tudjuk, hogy az első 48 dkg tömegű?

Amerikai feladat

(3 pont)

A beküldési határidő 2020. február 10-én LEJÁRT.

Megoldás. Egyensúlyban mindegyik rudacska bal szélét háromszor nagyobb erő húzza, mint a jobb szélét. Ezek szerint ha a 4. pingvin súlya \(\displaystyle G_4\), akkor \(\displaystyle G_3=3\,G_4\). A középső rudacska jobb szélét \(\displaystyle G_3+G_4=4\,G_4\), a bal szélét ennek háromszorosa, vagyis \(\displaystyle G_2=12\,G_4\) erő húzza lefelé. Végül a legfelső rudacskára ható erő a bal szélénél \(\displaystyle G_1=3\cdot 16\,G_4=48\,G_4.\) A feladat szövege szerint \(\displaystyle 48\,G_4\) megegyezik 48 dkg-nyi tömeg súlyával, így a többi tömeg: \(\displaystyle m_2=12~\rm dkg\), \(\displaystyle m_3=3~\rm dkg\) és \(\displaystyle m_4=1~\rm dkg\).

Statisztika:

81 dolgozat érkezett.
3 pontot kapott:	62 versenyző.
2 pontot kapott:	11 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2020. januári fizika feladatai