A G. 824. feladat (2023. szeptember)

G. 824. Egy \(\displaystyle \ell\) hosszúságú kígyó a hosszának feléig besiklott egy keskeny, egyenes csőbe. A kígyó kint lévő vége tetszőlegesen kanyaroghat a vízszintes talajon. Ha a kígyót homogén tömegeloszlású, \(\displaystyle \ell\) hosszúságú, hajlékony kötéllel modellezzük, akkor a sík mely pontjaiban lehet a kígyó tömegközéppontja?

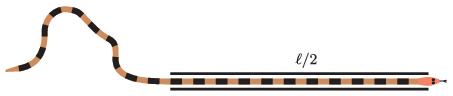
(4 pont)

A beküldési határidő 2023. október 16-án LEJÁRT.

Megoldás. Legyen a kígyó teljes tömege \(\displaystyle m\), ekkor (a tömegközéppont szempontjából) a csőben lévő része is és a kint kacskaringózó rész is egy-egy \(\displaystyle m/2\) tömegű tömegponttal helyettesíthető. Jelöljük a cső egyik végét (amelyiknél a kígyó feje van) \(\displaystyle A\)-val, a cső felezőpontját \(\displaystyle S_1\)-gyel, a cső másik végét (ahol a kígyó ,,közepe'' van) \(\displaystyle C\)-vel, a kígyó farkának helyét pedig \(\displaystyle B\)-vel (1. ábra).

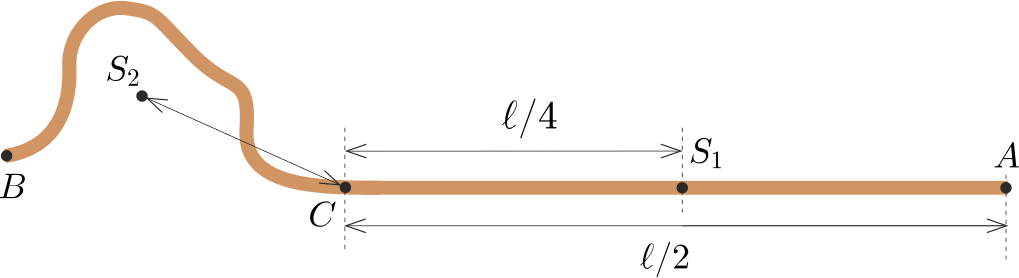
1. ábra

A kígyó első (egyenes) részének \(\displaystyle S_1\) tömegközéppontja \(\displaystyle C\)-től nyilván \(\displaystyle \ell/4\) távol van, a másik rész \(\displaystyle S_2\) tömegközéppontjának \(\displaystyle C\)-től mért távolságát pedig jelöljük \(\displaystyle r\)-rel. A kígyó alakjának ismerete nélkül \(\displaystyle r\) nagyságát nem tudjuk pontosan megadni, de azt állíthatjuk, hogy \(\displaystyle r\le \ell/4\). Ez – a továbbiakban fontos – egyenlőtlenség elég szemléletes (hiszen ha a kígyó kiegyenesedne, akkor éppen \(\displaystyle r=\ell/4\) teljesülne), de szigorú bizonyítását a Függelék tartalmazza.

Az egyenlőtlenséget felhasználva kétféle megoldás is adható a feltett kérdésre.

I. (geometriai) megoldás. A kígyó tömegközéppontja az \(\displaystyle S_1S_2\) szakasz \(\displaystyle S\) felezőpontjában található. Jelöljük \(\displaystyle CS_1\) felezőpontját (vagyis a cső nyolcadolópontját) \(\displaystyle P\)-vel (2. ábra).

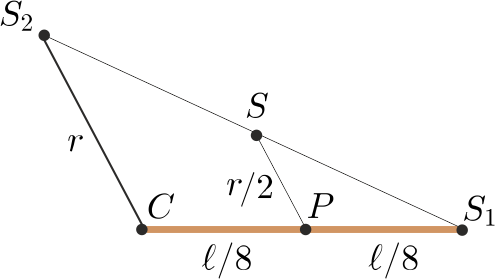
2. ábra

A \(\displaystyle CS_1S_2\) és a \(\displaystyle PS_1S\) háromszögek hasonlósága miatt

\(\displaystyle SP= \frac{r}2\le\frac{\ell}8.\)

Figyelembe véve, hogy a \(\displaystyle CS_2\) egyenes iránya tetszőleges lehet, megállapíthatjuk, hogy a kígyó \(\displaystyle S\) tömegközéppontja egy \(\displaystyle P\) középpontú, \(\displaystyle \ell/8\) sugarú körlapon található.

II. (vektoralgebrai) megoldás. Jelöljük a \(\displaystyle \overrightarrow{CS_1}\) vektort \(\displaystyle \frac14\boldsymbol{\ell}\)-lel, a \(\displaystyle \overrightarrow{CS_2}\) vektort pedig \(\displaystyle \boldsymbol r\)-rel. Ekkor \(\displaystyle C\)-ből a kígyó \(\displaystyle S\) tömegközéppontjába mutató vektor

\(\displaystyle \boldsymbol s=\frac12\left(\frac14\boldsymbol{\ell}+\boldsymbol r\right)= \frac18\boldsymbol{\ell}+\frac12\boldsymbol r.\)

Innen leolvashatjuk, hogy \(\displaystyle S\) és \(\displaystyle P\) távolosága

\(\displaystyle \left|\boldsymbol s- \frac18\boldsymbol{\ell} \right| =\frac12|\boldsymbol r|\le \frac{\ell}8.\)

A kígyó \(\displaystyle S\) tömegközéppontja tehát egy \(\displaystyle P\) középpontú, \(\displaystyle \ell/8\) sugarú körlapon (a 3. ábra sárga tartományában) helyezkedhet el.

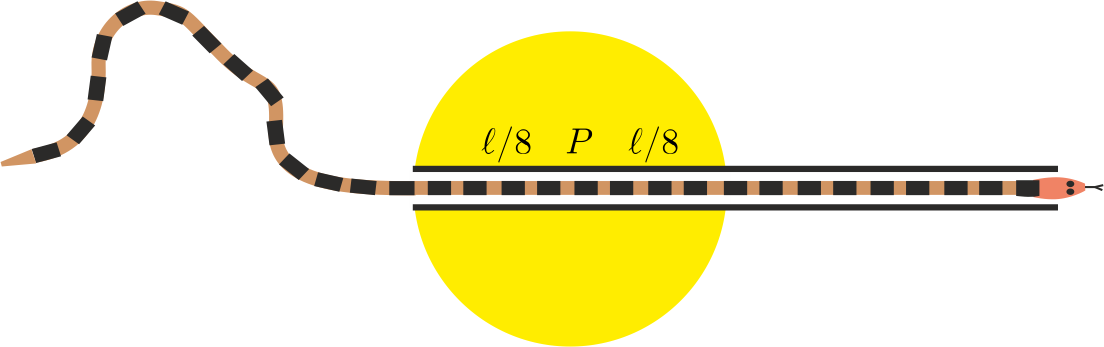
3. ábra

Függelék. Tekintsük a kígyó hátsó felét a \(\displaystyle C\) és \(\displaystyle B\) pontok között kanyargó görbe vonalnak, aminek tömegközéppontja \(\displaystyle S_2\). Ha a ,,félkígyó'' kiegyenesedne, és a \(\displaystyle CS_2\) egyenessel párhuzamos \(\displaystyle CB'\) lenne, akkor az \(\displaystyle S_2'\) tömegközéppontja \(\displaystyle C\)-tól \(\displaystyle \ell/4\) távolra kerülne.

Hasonlítsuk össze a kanyargós kígyó tetszőleges \(\displaystyle P\) pontját ugyanezen pontnak a kiegyenesedett kígyón megtalálható \(\displaystyle P'\) megfelelőjével (4. ábra). Nyilván \(\displaystyle CP\le CP'\), továbbá \(\displaystyle CP''\le CP\) (ahol \(\displaystyle P''\) a \(\displaystyle P\) pont merőleges vetülete a \(\displaystyle CB'\) egyenesen), és így

\(\displaystyle CP'\ge CP\ge CP''.\)

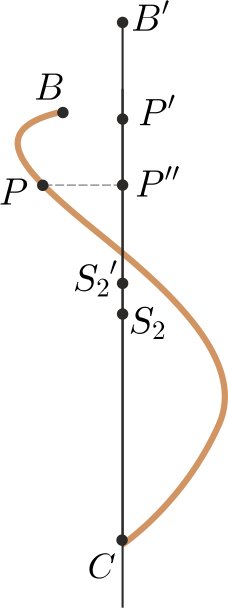
4. ábra

A görbe félkígyó tömegközéppontját a \(\displaystyle CP''\) távolságok határozzák meg. Mivel a fenti egyenlőtlenség minden \(\displaystyle P\) pontra érvényes, a tömegközéppontokra is fennáll:

\(\displaystyle r=CS_2\le CS_2'=\frac{\ell}4,\)

és éppen ezt akartuk bizonyítani.

Statisztika:

42 dolgozat érkezett.
4 pontot kapott:	Blaskovics Ádám, Bohner Emese, Bús László Teodor, Csizmadia Ferenc, Derűs Ádám , Field Márton, Fülöp Magdaléna, Hajdufi Imola, Klenkó Éva Borbála, Méhes Mátyás , Porcsin Gréta, Pulka Gergely Tamás, Szabó András, Tajta Sára, Varga 511 Vivien.
3 pontot kapott:	Gerlei Dániel, Schmidt Marcell, Sipos Dániel Sándor, Táborosi Sára.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	5 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	6 dolgozat.

A KöMaL 2023. szeptemberi fizika feladatai